勉強しているのに成績が伸びない理由
- 2023.02.18

まとめから
| 伸びる人 | 伸びない人 | |
|---|---|---|
| 練習量は | 多い | 少ない |
| やってる勉強は | 学力に合っている | 学力に合っていない |
| 「できた」の定義は | 満点 | 高得点 |
| 塾や問題集は | 1つに絞る | 複数使う |
| ヤル気がないときに | 勉強する | 勉強しない |
| 当たり前のことを | 大事にする | 軽視する |
| 勉強する理由は | 自己実現 | 他者承認 |
| 情報の入手は | お金と足 | 無料で指先 |
練習不足
たとえば野球で打撃(バッティング)の練習をするとします。上手な選手の打撃を見たり良いコーチを受けたことで打てるようになっても、その段階で練習をやめてしまったら試合で打てるわけがありません。
当たり前すぎる。
具体例
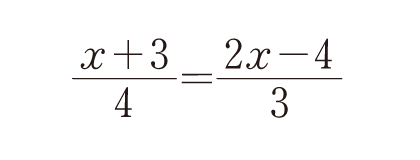
中1の一次方程式の基礎ですね。
これの習得には500~1000問の練習が要ります。
そ、そんなにっ!?
宿題のプリントやテキストを1回撫でるだけでできるわけがない。
やっている勉強が学力に合っていない
その教科書を学ぶ上で必要な前提知識や処理能力が足りていないということです。
具体例

2017年に静岡学園中学で出題された問題。表にまとめると規則がみつかるのですよね。
F(n)=F(n-1)+n
Fが分割数、nが線数
「弦による円分割」という漸化式(数2B)の定番例題です。
高校数学!
「表にして規則を見つける」のが前提であり、さらにその前提がこの画像です。
そういう過程を経ないと公式覚えたところで問題は解けないです。
宿題でよくある負のスパイラル
- 定期テストや通知表が気になるのでとにかく宿題をやる
- スムーズに解けないので時間がかかり、ストレスに耐えかねておざなりに処理する
- 時間がかかるので勉強した気にはなるものの、実際の消化量は少ない(学習量が不足する)
- 理解が中途半端なので結局テストで点はとれない
- 頑張りが報われないので勉強そのものに嫌気がさす
この悪循環から抜け出す方法は、「夏休み等を利用してやり直す」か「学力層が低い学校やクラスを選ぶ」の二択。
学校選び、大事!
「できる」の定義が間違っている
問題が解けることとテストで点がとれることは違います。
「解ける=できる」と認識しているうちは・・・
- 計算ミスなどのケアレスミスが無くならない
- 単元横断の総合問題に手が出ない
できた気になるので練習量が不足するわけです。

塾や問題集に手を出し過ぎ

ドラゴン桜2(講談社)
まぁ、真実ですね。
ヤル気で勉強している
成績上位者はヤル気がなくても勉強します。
気分が乗らなくても勉強するから伸びるわけです。
食欲がなくても食べなければ体力が下がるのと同じです。
そもそも「ヤル気出せ」という言葉が間違っている
ヤル気とは本人の欲求と行動がリンクすることで自然発生するものであり、「出せ」と言われて出てくるものではないです。
社員や部下をタダ働きさせたい会社が使い始めたというのが有力説です。
ブラック反対!

改変履歴
- 【2023.02.18】刷新に併せて項目以下と簡素化。
- 【2022.06.30】新装版に変更。
- 【2022.01.16】文脈修正と補足解説の追記。
- 略
- 【2019.10.22】初版
