面積公式を組み合わせて解く半円の面積計算
- 2021.06.08
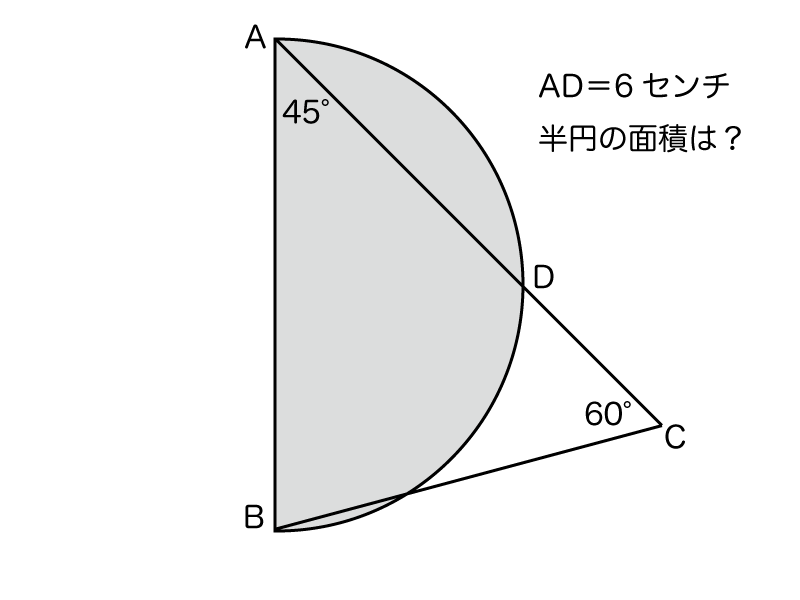
小学4~5年生で習う図形の基礎知識を複雑に組み合わせて解きます。
偏差値55-(高難度)
- 三角形と四角形の性質(小学4年生)
- ひし形の面積(小学5年生)
- 円の面積(小学5/6年生)
- 円周角の定理(中学生)
まずはヒント
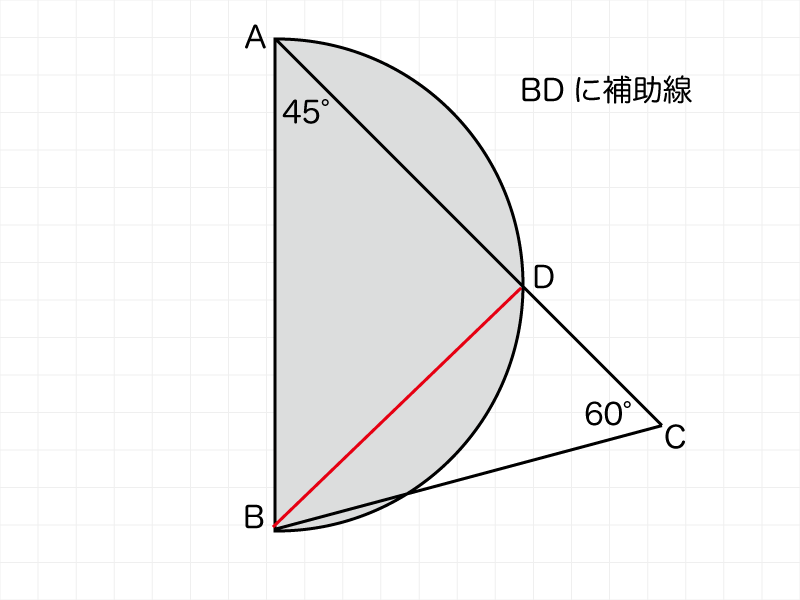
ここに補助線を引きます。
補助線は本来「気づき」ですが、この類の問題をたくさんこなしている人なら「知識」で解決できます。
そういうのはあんまり良くないと思うけど、受験するならしかたない。
三角定規を見つける
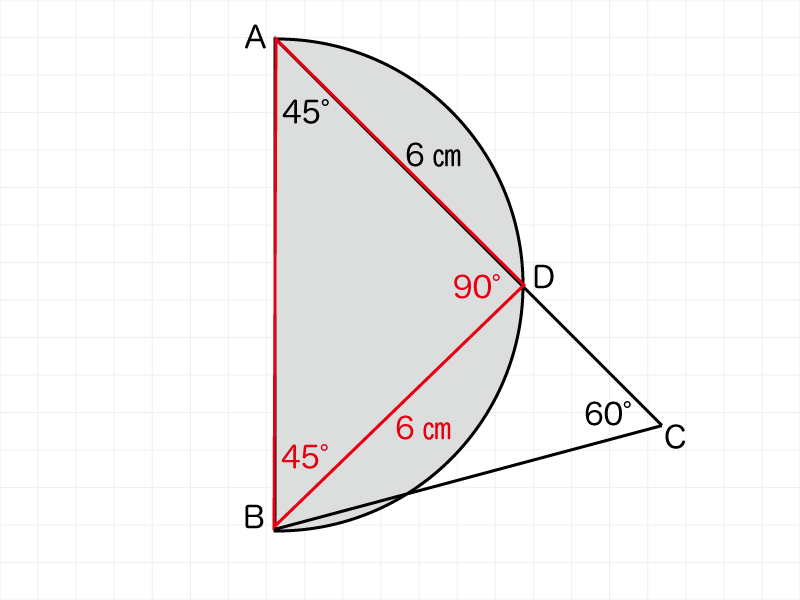
補助線をひくことでABDに二等辺三角形があらわれます。この二等辺三角形は45°の三角定規と同じ形状です。
どうして二等辺三角形なの?
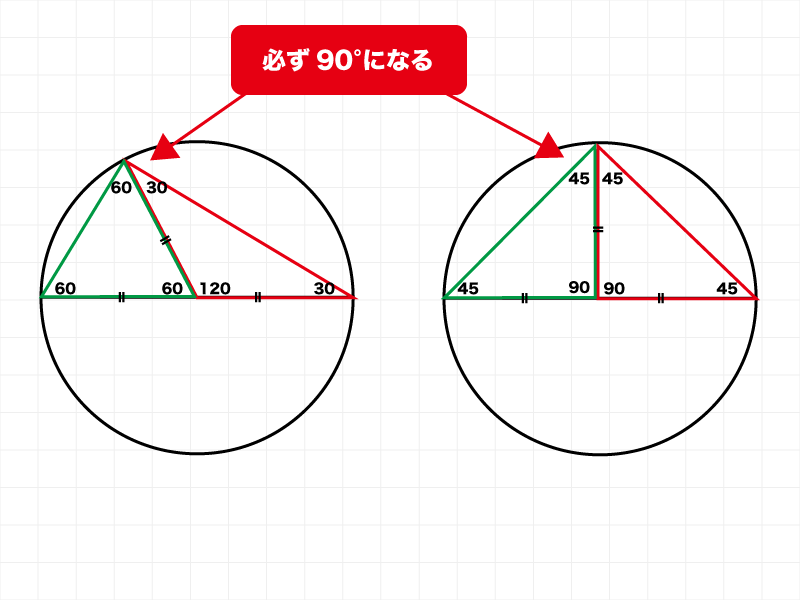
円の直径の両端からひいた線の円周接点は必ず90°になる
中学生で習う「円周角の定理」のしくみです。文字で説明すると雑多になるので図で解説します。
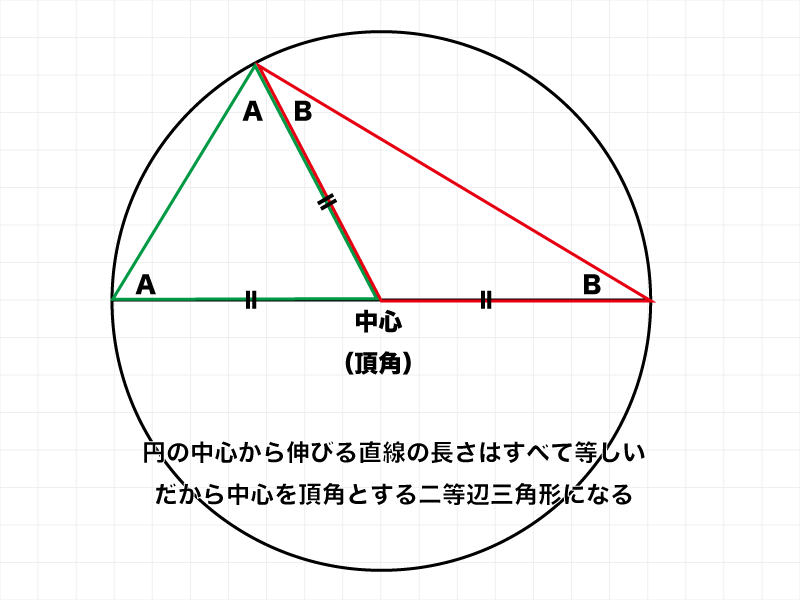
中心を頂角とした残り二辺の長さは等しくなります。(円の半径ですから)
ここの角AとBについて考えてみます。
- 三角形の内角の和は180°。赤と緑の2つの三角形があるので角度の合計は360°
- そのうち、中心点に接している角度、つまり二等辺の頂角の角度は赤と緑合わせて180°(2つで直線になっています)
- つまり残りの角度の合計は360-180=180°
- つまり角A+角A+角B+角B=180°
- つまり角A+角B=90°
- 角Aと角Bがそれぞれ何度かは不明でも、ふたつ合わせて90°、隣接している箇所は直角。
だから円に接している部分の角度は90°=直角になります。
正方形の面積公式
補助線を引いたことで45°の三角定規を見つけることができました。
設問の図形は「半円」ですから三角定規も「何かの半分」かもしれません。
受験算数でその発想はお約束。
45°三角定規は組み合わせると正方形になる
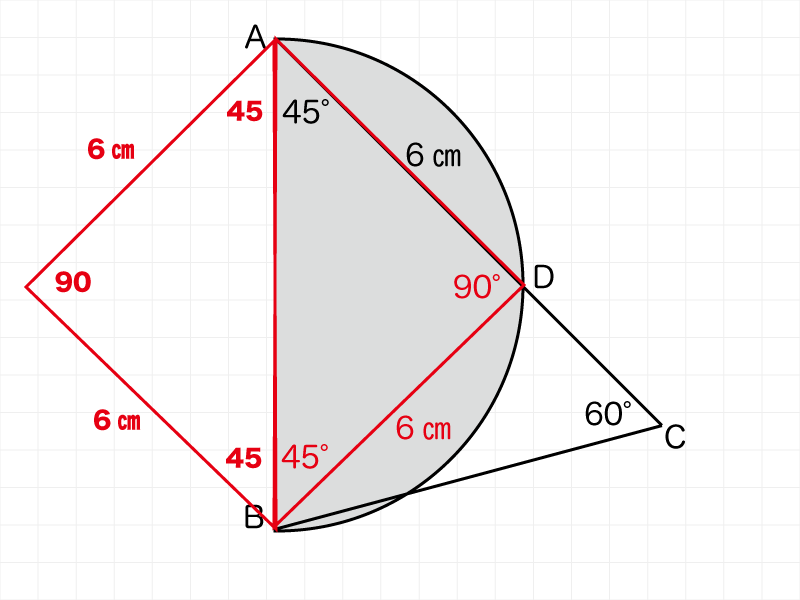
三角定規を線対称でコピーすると正方形ができます。
与えられている長さの部分が正方形の一辺なので、とりあえず面積を出しておきます。
6 × 6 = 36
正方形はひし形の公式でも面積が出せる
〔面積〕=〔一辺 × 一辺〕 =〔対角線 × 対角線 ÷ 2〕
| 式 | 答え | |
|---|---|---|
| 正方形公式 | 一辺 × 一辺 | 36 |
| ひし形公式 | 対角線 × 対角線 × 1/2 | 36 |
この図形の場合、対角線×対角線=72です。これが64や81だったら平方数(8×8や9×9)で対角線の長さが求められますが、今回の数字はむりなようです。
円の面積公式
半径 × 半径 × 3.14 ですが、その「半径」を視覚的に考えます。
着目点は「ひし形」の対角線です。
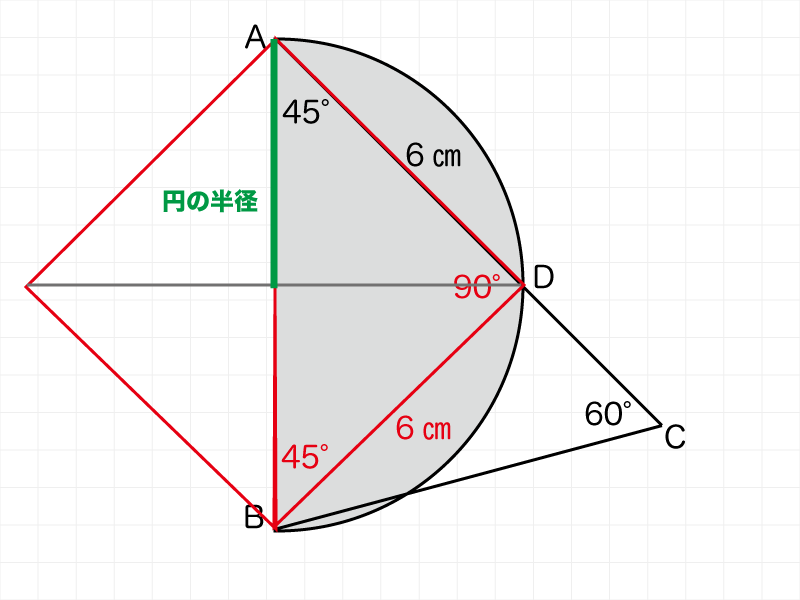
わかりやすいように緑色にしてみましたが、円の半径はひし形対角線の1/2です。
であれば、半径 × 半径 × 3.14 は次のように書き換えることができます。
〔対角線 × 1/2〕×〔対角線 × 1/2〕× 3.14
これについて・・・
〔対角線 × 1/2〕×〔対角線 × 1/2〕× 3.14
赤文字の部分は先ほどのひし形の計算で「36」であることがわかっています。
つまり・・・
〔36〕×〔1/2〕× 3.14
これで円全体の面積が求められます。
設問は半円なので、さらに1/2すれば答えが出ます。
〔36〕×〔1/2〕×〔1/2〕× 3.14
9 × 3.14 = 28.26
難しいと思うならこちら
Extremeさらに深部へ
この部分の面積を出してみましょう。
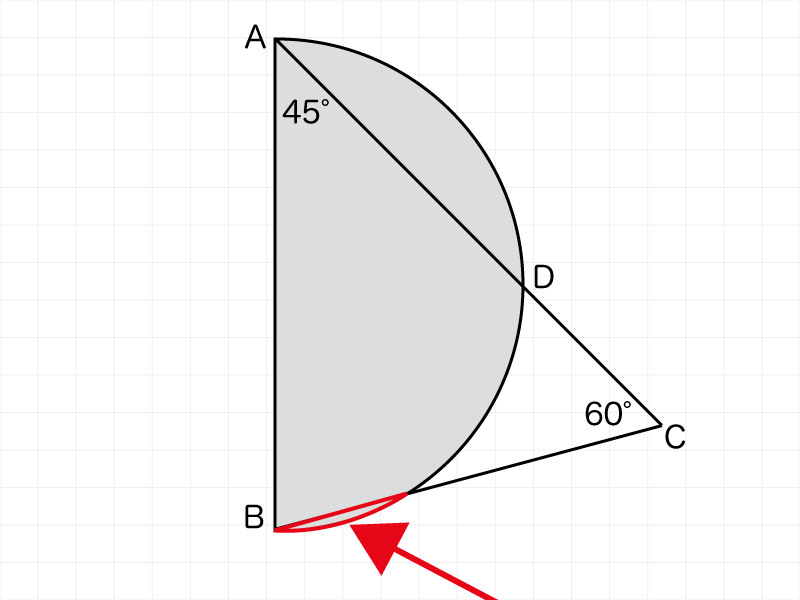
ヒントのみ
ここで角Cの60°の出番です。
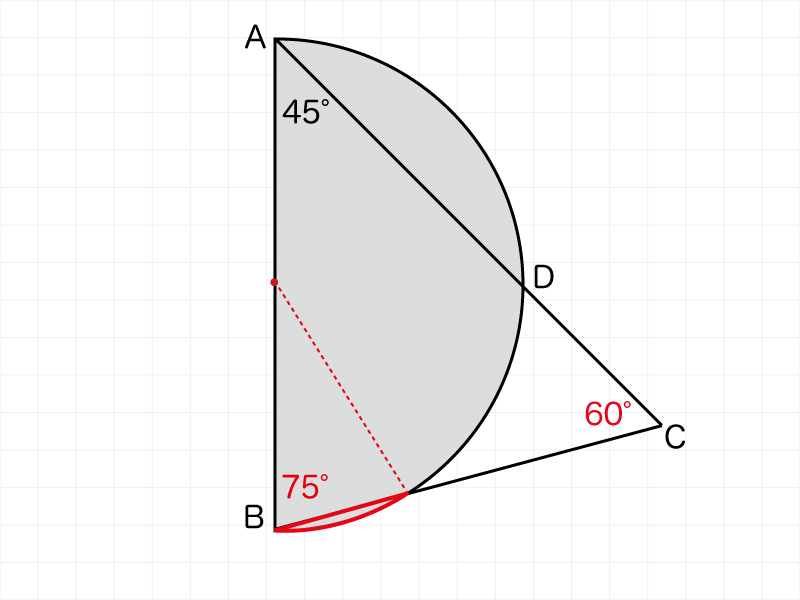
上の図のように中心点から補助線をひいておうぎ形をつくります。
おうぎ形の面積から三角形の面積を引けば求められることまではわかると思います。
三角形の面積は、点Bの角度によっておうぎ形の中心角があの角度になることがわかれば・・・
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)