合同条件で解く角度計算
2020.07.20
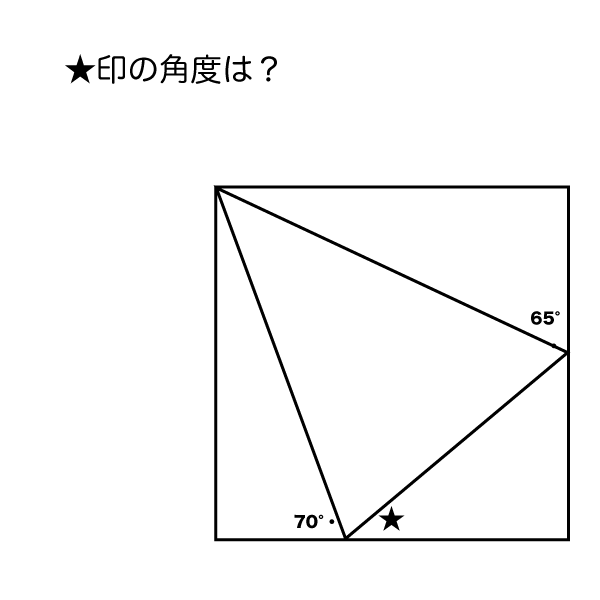
〔問題補足〕図の四角形は正方形です。
見かけシンプルですが、結構な難問だと思います
- 対称・合同(小学6年生)
解き方
まずはわかっている角度を埋めてみます。
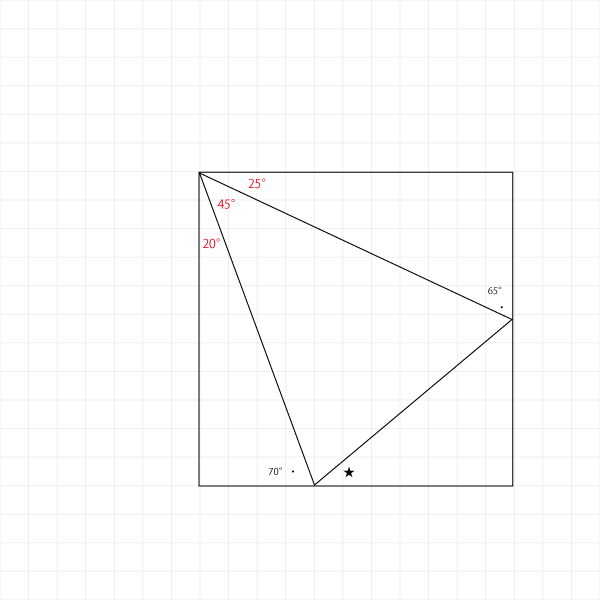
うーん、これだけじゃ何ともなりませんねぇ・・・
つぎたす・入れ替える・まわす・反転する
情報が足りないなら自分でつくることを考えます。
図形の一部を「つぎたす・入れ替える・まわす・反転する」ことを問題用紙の上でシミュレートするために使うのが補助線です。
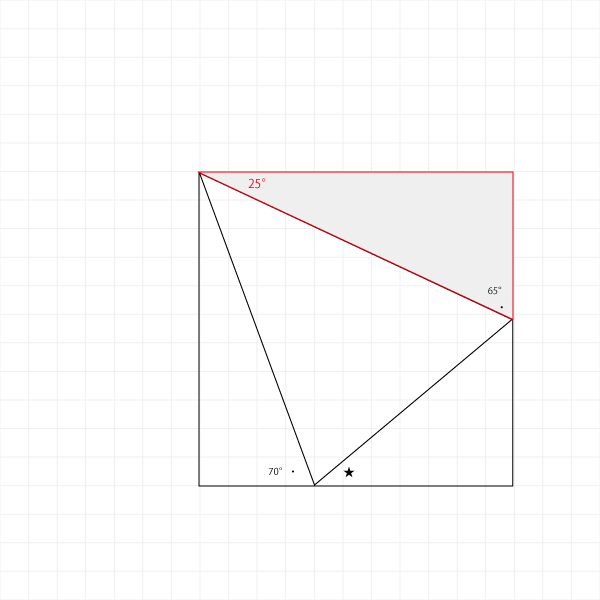
赤枠で囲った三角形をどうにかしてみます。
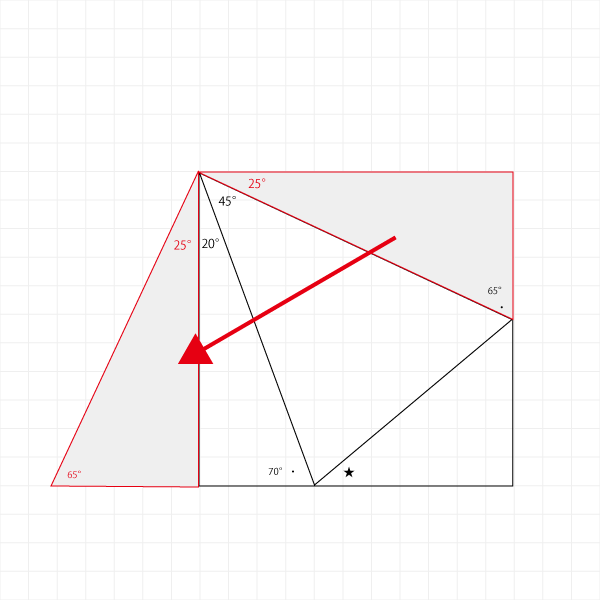
こんな感じで移動してみます。
このとき、移動した三角形の各辺の位置を忘れないようにしましょう。慣れていないうちは記号をつけたり色ペンでなぞるといいです。
動かしたら、ここに注目です。
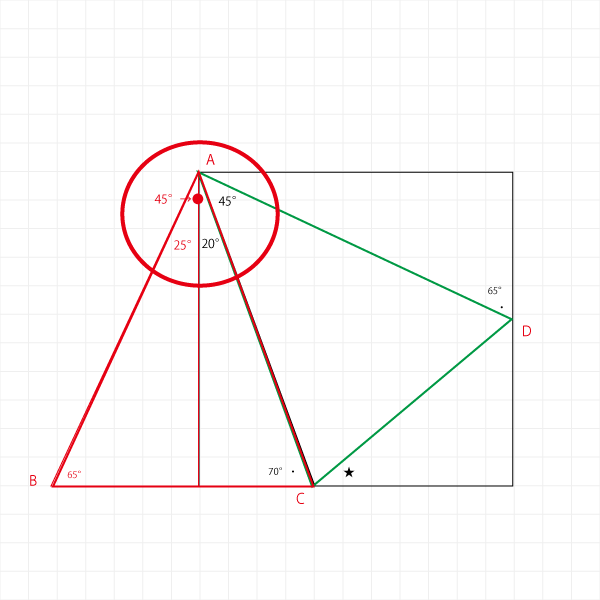
一部頂点にABCDの記号をつけました。
線BCを底辺とする三角形の頂点Aの角度は、25°+20°=45°になっています。
すぐ右隣りに似たよーな角度がありますが、ここに気づけるかどうかがこの問題のひとつの要所です。
合同をみつける
三角形ABC(赤)と、三角形ACD(緑)の中間点、つまり線ACのラインをそのまま伸ばしてみると・・・
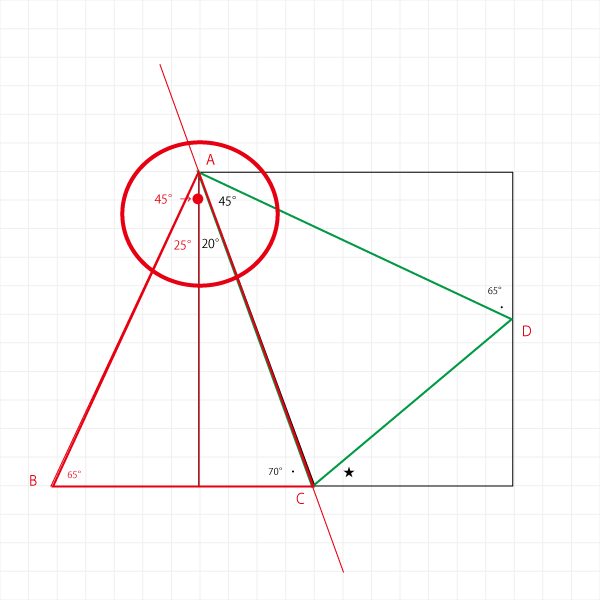
このふたつの三角形は線対象になっているようです。
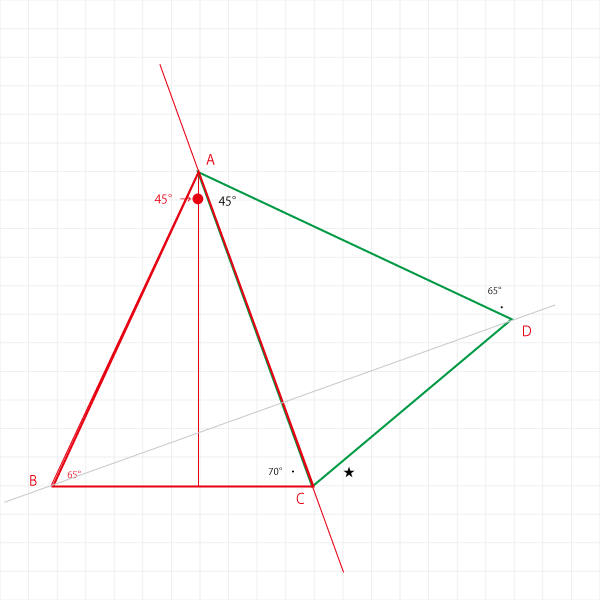
線対称かどうかは定規や方眼紙で確認が要りますが、合同条件を満たしているので赤線と緑線は合同な図形といえます。
合同条件
- 三辺の長さがすべて同じ
- 二辺の長さとその間の角度が同じ
- 一辺とその両端の角度が同じ
それがわかればこのあたりの角度も埋められます。
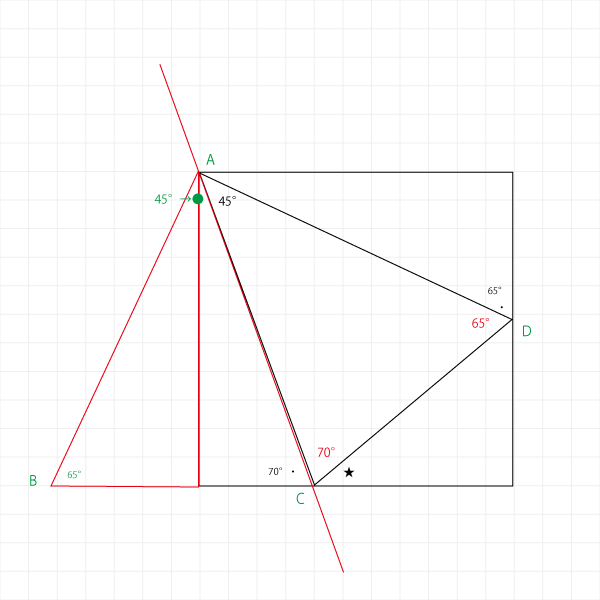
ここまで埋まれば★の角度も出せますね。
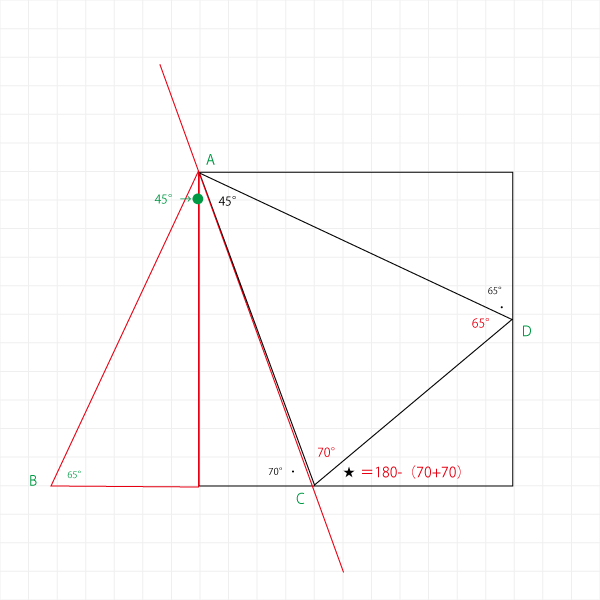
180°-70°-70°=40°
別解?作問者になってみる
45°の頂点Aから底辺BCに向かって垂直の線を伸ばしていくと、この三角形は正方形の対角線から少し傾いていることがわかります。
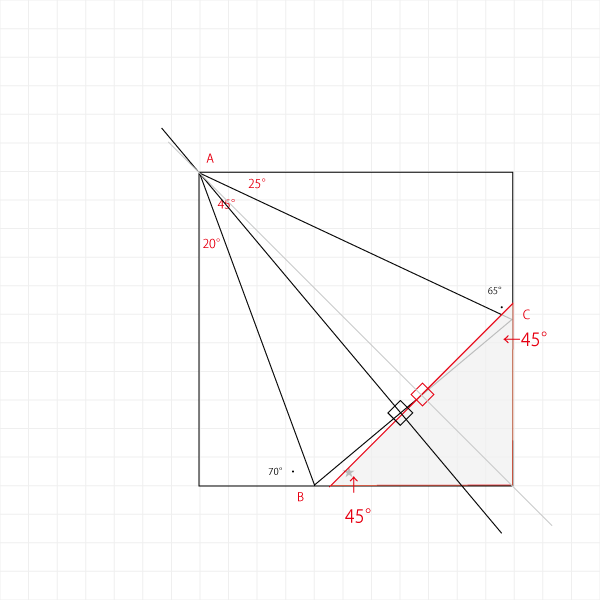
頂点Aの「45°」を変えずに傾きを修正すると・・・
- 点Bの70°は67.5°(2.5°小さくなる)
- 点Cの65°は67.5°(2.5°大きくなる)
「A45°、BC67.5°の二等辺三角形を傾けて作成している」と考えれば、その過程を再現することで答えを出すことができそうです。
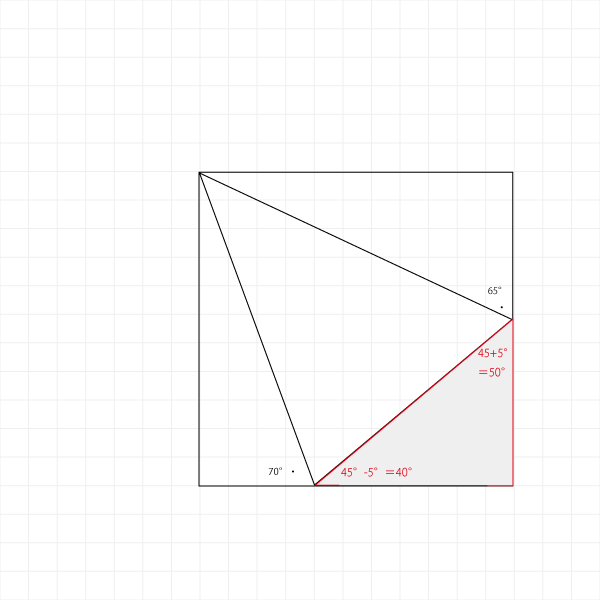
では、何度傾ければいいのかというと、点Bを元に考える場合・・・
- 点Bから2.5°小さくなっている
- 点Cが2.5°小さくなるので追従してさらに2.5°小さくなる
つまり、対角線状態の45°から合計5°を引いてやればよいです。
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)
