円周率は「3.00」以上であることを証明せよ
- 2020.03.11
円周率は「3.00」以上であることを証明せよ
2003年の東京大学入試で出題された超有名な問題を、小学生でも解けるように数字を少し変えたものです。
ちなみにオリジナルはこうです。
円周率は 3.05 以上であることを証明せよ
オリジナルが「3.05」に対して「3.00」ですが、考え方や手順は同じです。
偏差値55-
- 円周率(小学5年生)
- 多角形の角度(小学5年生)
正多角形の角度と作図(小学5年生)
この類の証明問題は「具体的な何かを引き合いに出して比較する」という流れで解きます。
数学でいう「証明」の書き方は中学生で習います。小学生は図表や計算式や言葉をつかって説明できればよいです。
この問題を解くために引き合いに出すのは・・・
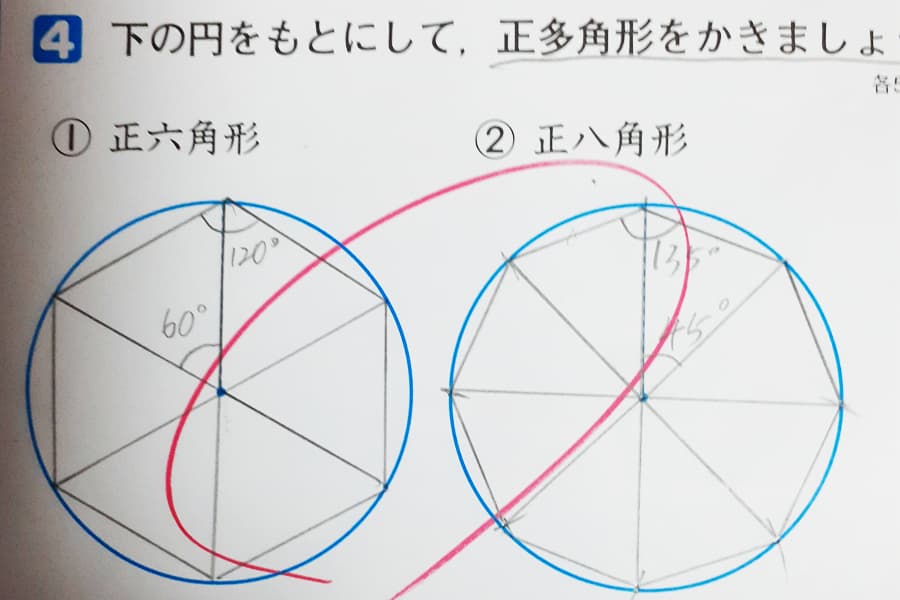
小学5年生の教科書や基礎問題集に必ず出てくるアレです。
問題文を読んでこの図が思い浮かべば解けたも同然です。
円周率が「3.00」より大きい証明
- 円に内接して正六角形を描く。
- 一般的な描き方では描く過程で正三角形ができる
- 正三角形の一辺は六角形の一辺と同じなので、半径を「1.00」とすれば六角形の外周は6.00。
- 同様に正三角形の一辺は円の半径でもあるので、円周は2×円周率
- 六角形は円に内接しているので長さの関係は「円周>六角形外周」の不等式になる。
- つまり「円周の2倍>6.00」→「円周>3.00」。
- 「円周>3.00」を言葉で読むと、円周率は3.00より大きい…
「3.05」の場合(オリジナル)
- 正八角形を使う
- 一辺の長さを余弦定理で求める( √1+1-2cos45°)
- 8倍して√をバラすと「6.12...」
- 「2π>6.12」→「π>3.06」
算数では八角形の一辺が求められないので、この部分だけ高校数学です。
あとがき
今やネタ問題のように扱われている伝説的問題です。
出題された2003年はゆとり教育で「円周率=3.00」で物議がわきおこっていた時期であり、それに対する東大の意思表明だという見解も見かけますが、それを受験者に伝えるためだけに1問使うとは・・・・思えません。
であればこの問題が試しているのは、問題文を読んでこの図が思い浮かぶか?・・・ではないかと。
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)
