九九表の数字を全部足すといくつ?

- 2025.12.22
九九表(9×9)の数字を全部足すといくつ?
昨年(2024年)まではあまり知名度はなかったものの、ある理由で今年になって一気に有名になった問題です。
以下は解法解説です
答えと解説
2025
この問題は答えが「2025」になるので、2025年度入試で出題した中学校や高校が複数あったようです。
等差数列の和中学受験では定番の高校数学
1+2+3+…+8+9の計算方法はご存じ?

| 1 | 2 | 3 | 4 | 5 |
| 9 | 8 | 7 | 6 | |
| 10 | 10 | 10 | 10 | 5 |
(10×4)+5=45
あるいは…
| 0 | 1 | 2 | 3 | 4 |
| 9 | 8 | 7 | 6 | 5 |
| 9 | 9 | 9 | 9 | 9 |
9×5=45
余裕があるなら〔最初の数+最後の数〕×〔数の合計〕÷2だって覚えましょう。(等差数列の和)
〔最初の数+最後の数〕×〔数の合計〕÷2
(1+9)×9÷2=45
等差数列(の和の公式)は、教科書では高校1年生頃ですが、中学受験教材では小学4年生以上の問題集に収録されています。
各段の合計を求める
直前の計算は九九表の「一の段」の合計を求めています。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
続けて二の段も計算します。
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
(2+18)×9÷2=90
なのですが、ここはあえて次のように表記して考えます。
- (1+9)×9÷2=45
- (1+9)×9÷2=45
二の段の合計は、一の段の「2倍」と示しているのかな
引き続き三の段です。
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
ここまでをひとつのリストにまとめてみます
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
〔45×6=270〕
その「×6」は、最終的にいくつになるでしょう?
もう一回、等差数列
〔(1+9)×9÷2=45〕×n…として、
一の段は「×1」、二の段は「×2」、三の段は「×3」だから、最後の九の段は「×9」になるはずです。
九の段のイメージ
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
- (1+9)×9÷2=45
×45!
最初に一の段の計算でやったから計算不要ですね
- {(1+9)×9÷2}×{(1+9)×9÷2}
- 45×45=2025
各段の合計が「一の段のn倍」というところまでは気づけますが、そのnも等差数列で処理すればいい…というのは解き終わってからでなければ気づきにくいかもですね。
おまけ:検算
- 2025を素因数分解する
- 3×3×3×3×5×5
→(3×3×5)×(3×3×5) - 45×45
等差数列でつくった計算式と一致
素因数分解は、現在(2025年)の教科書では中学1年生ですが、中学受験教材では約数倍数の話で出てくるので小学4~5年生です。
別解
- 九九表を4枚用意して、それぞれABCDする
- 各シートを90度ずつ回転させて重ねる
左上のマスにある4枚を見ます。正方向では「1×1=1」のマスです。
指定座標の4枚を透かして見る感じです
- 1×1=1
- 1×9=9
- 9×9=81
- 9×1=9
このマスのABCDの合計は「100」です。
他のマスも見てみましょう。正方向で「2×3=6」のマスを見てみます。
- 2×3=6
- 7×2=14
- 7×8=56
- 8×3=24
これもABCDの合計は「100」です。
1マス100で、九九表は81マスだから…
100×81マス÷4枚=2025
クイズ的な解き方ですね
アクティブラーニングなら思考訓練になるかもしれませんが…
九九表の問題は規則的な反復計算を公式で単純化できることを体感しやすいので、クイズ的解法ではなく前半で紹介した手順で勉強するのがお勧めです。
中学受験の入試問題における数列の出題や問題集や学習指導について思うこと
今回扱った「等差数列の和」は「折り返し」のイメージで小学生にも理解しやすいですが、 「黄金比を感じる美しい数字の並び、それがフィボナッチ数」という話の流れで階差数列(高校2年生以降)を持ち出したり、 等比数列や階差数列がアリなら漸化式(共通テストのラスボス的存在)もやってしまえ…という感じで講師も教材も暴走しやすいのが中学受験の数列だと思います。
フィボナッチ数とは隣り合わせた数字の和が次の数字になる数列。
1,1,2,3,5,8,13,34,55,89…
漸化式もどき(弦による円分割)
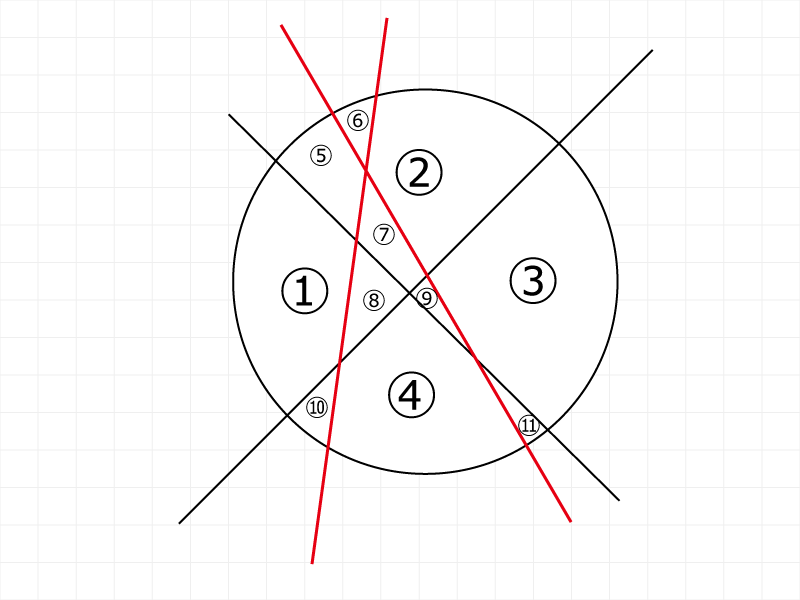
こういう解説ページや解説動画をつくる人は自己の解説に酔いやすい性格をしてると思うので、私も気を付けています
すでに暴走してるぞ…
改変履歴
- 【2025.12.22】初版