正方形と正三角形が組み合わさった図形の面積計算30度150度の二等辺三角形をやっつける
- 2020.06.09
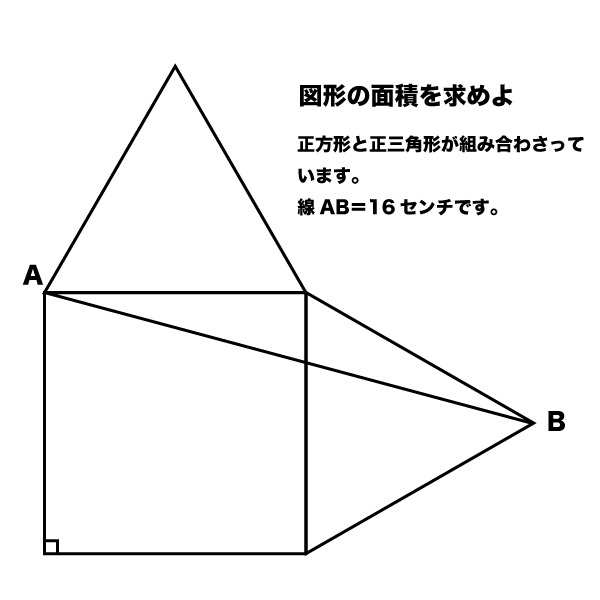
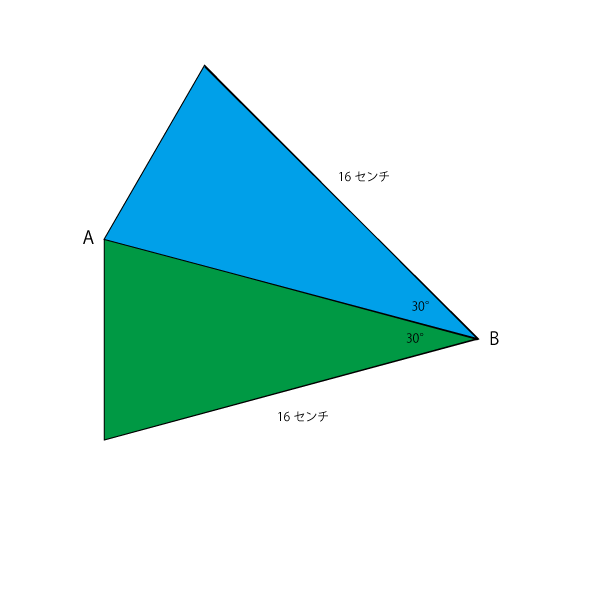
正方形と正三角形が組み合わさっています。線AB=16センチです。
図形の面積を求めよ。
正方形と正三角形が合体していて対角線(らしき)ラインが入っている問題は主に角度計算で出題されますが、この問題は「面積」なので難問の部類です。
偏差値55-(高難度)
- 三角定規(小学4年)
- 角度の計算(小学4年)
- 三角形と四角形の面積計算(小学4/5年)
前提知識30°と150°の三角形の面積計算
この問題は三角定規を補助線にした角度計算が前提知識になります。
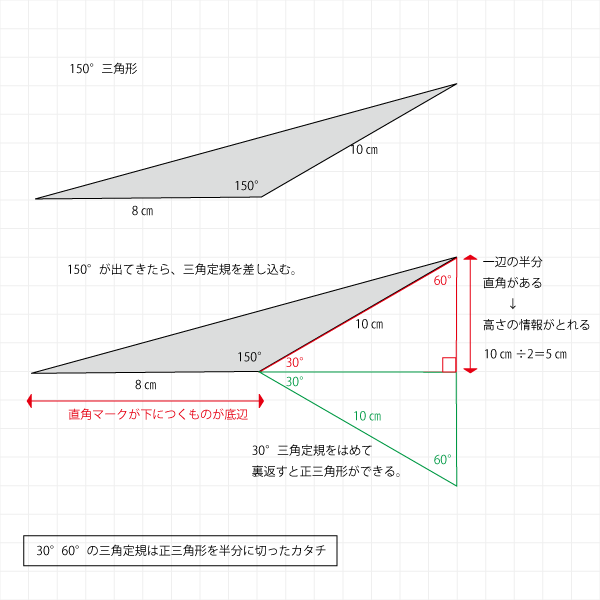
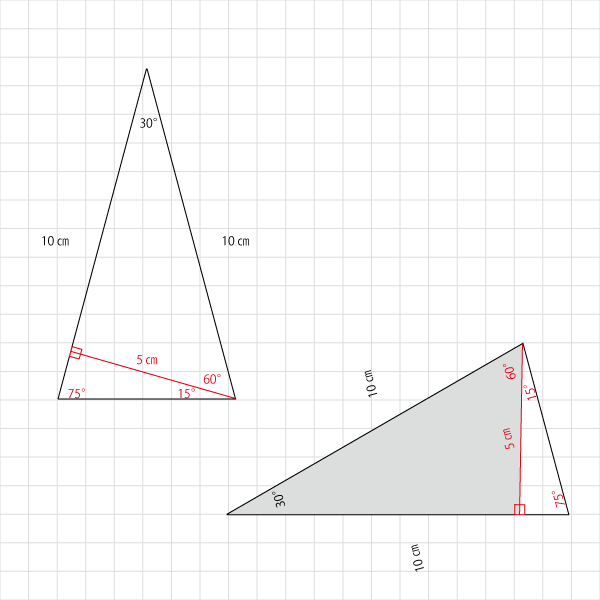
角度を確認する
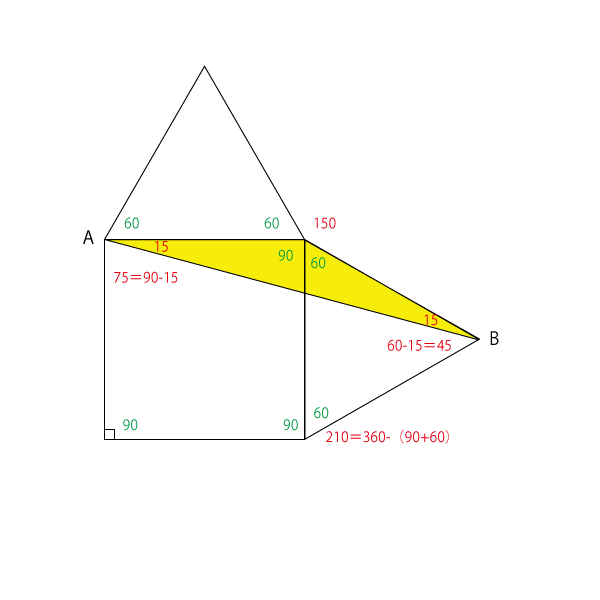
黄色で塗った三角形に着目します。
正三角形と正方形を構成する辺の長さは全て同じなので、色塗りの三角形は二等辺三角形であることがわかります。
30度二等辺三角形をつくる
〔15-15-150度〕の三角形の見かけ上の底辺となる線ABは、正方形の一角から三角形の最も遠い頂点に向かっています。
そこで、同じ条件で補助線をひいたのが次の図。
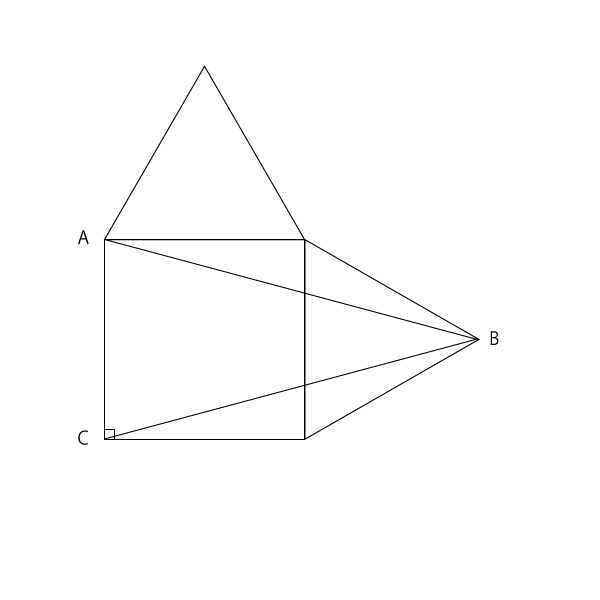
「AB=16センチ」という条件が与えられていますので、ABCを結んだ三角形は2つの斜辺がそれぞれ16センチの二等辺三角形であることがわかります。
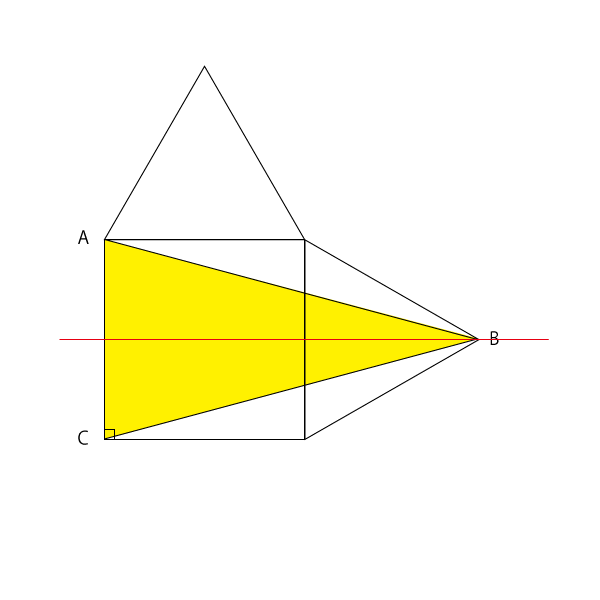
点Bの角度は、正三角形の1角60°から150°三角形の15°ふたつ分を引くと30°であることがわかります。
補助線で30°二等辺三角形をもうひとつつくる
ここに補助線をひく
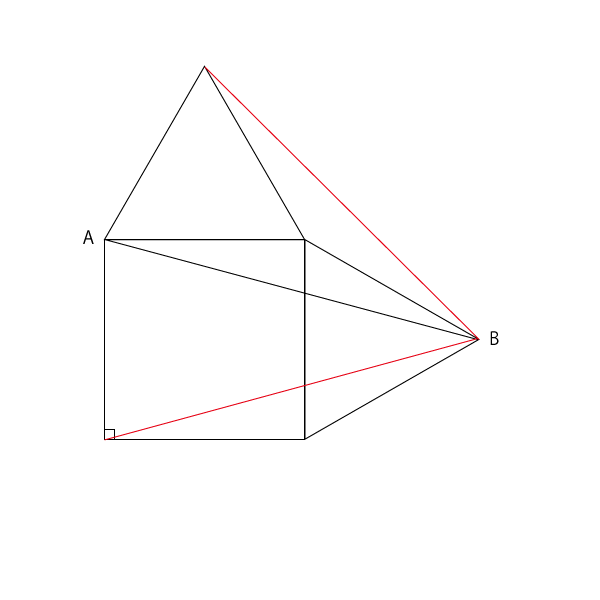
補助線でできたスキマに図の150度二等辺三角形を移動する
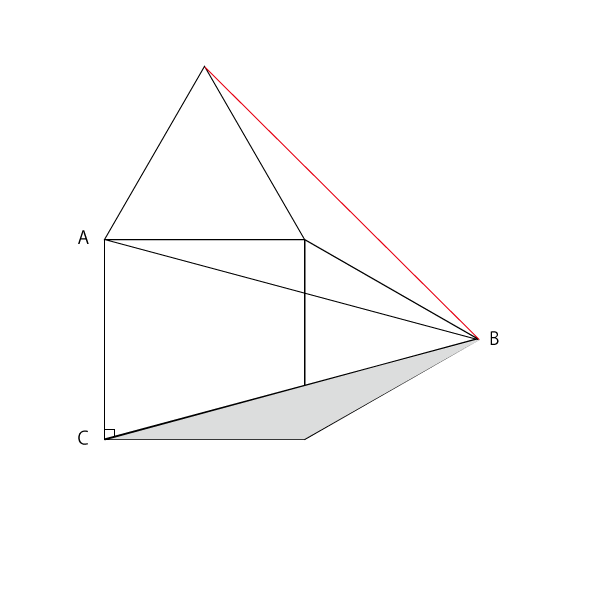
すると、こうなります。
30度二等辺三角形がふたつできました。
斜辺に数字が入っているので計算は簡単です。
- 青:斜辺16×(斜辺の半分8)÷2
- 緑:斜辺16×(斜辺の半分8)÷2
青64 + 緑64 = 128
ちなみに隠しコマンドを使うと・・・
(16×16÷4)×2 → 16×16÷2 いろいろにこむ(16×16=256)の半分で128
別解ひし形の公式で解く
(仕上げをわかりやすくするために)三角形の位置を変えます。
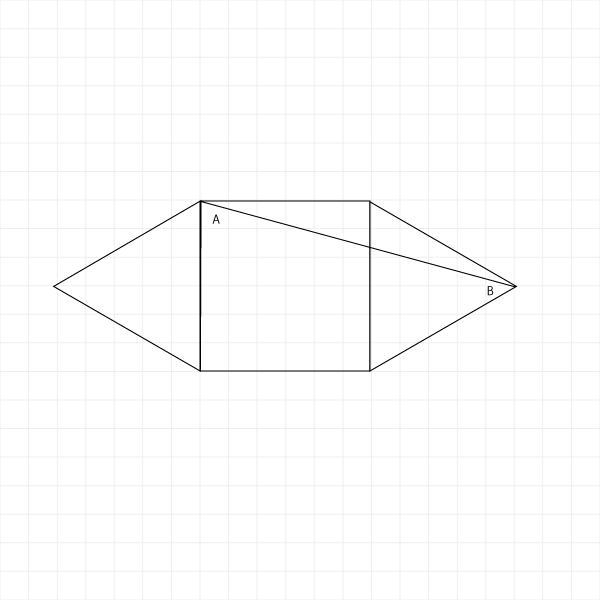
面積系ではこっちのほうがよく見かける並べ方です。
次に、線ABが対角線になる正方形を補助線として書きます。

書いたらそれを元の図の中心に移動。
直線ABを三角形の傾きに沿って二等分線まで並行移動です。
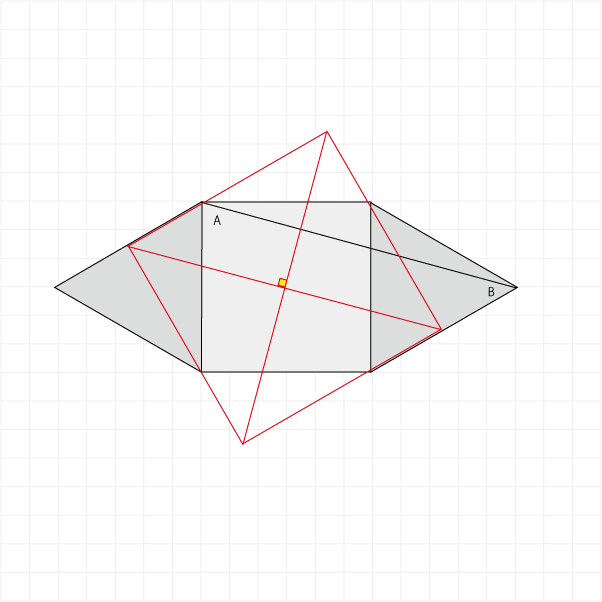
はみ出した部分は「30-60-90」の三角定規であり、補助線正方形の空いている箇所に納まります。
縦横の長さはわかりませんが、対角線の長さがわかっているのでひし形の公式で解けます。
対角線×対角線÷2=面積
16×16÷2=128(㎝2)
こういう問題や解き方は手裏剣や風車と呼ばれたりもするようです。
あとがき
最後の手裏剣ですが・・・
- 直感的でない補助線の使い方は小学生には難しい
- 解説の途中で「あ、わかったかも?あとは自力でやってみる」の入る余地がない
- 「このように手裏剣で解けるのです。では類問やってみましょ」という流れだと「できた気」になりやすい
授業や教材ではなくクイズ番組向けのような気がします。
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)


