静岡雙葉中学の受験対策
- 2024.03.01
静岡雙葉中学の受験対策概要
| 入試問題の難度 | 難しい |
|---|---|
| 志願倍率 | 低い〔定員割れ〕 |
| 専門対策の有効性 | 非常に高い |
| 総合難度 | やや難しい |
入試問題の難度
中学受験標準難度の範囲であるものの、県内では上位の難度です。
「専門対策の有効性」も併せてチェック。
志願倍率の傾向
浮き沈みがあるものの定員を下回りますが全入(大過なければ全員合格)ではありません。例年若干名の不合格者が出ています。
| 定員 | 志願者数 | 倍率 | |
|---|---|---|---|
| R6 | 150 | 110 | 0.73 |
| R5 | 150 | 138 | 0.92 |
| R4 | 150 | 130 | 0.86 |
| R3 | 150 | 105 | 0.70 |
| R2 | 150 | 151 | 1.01 |
| R1 | 150 | 172 | 1.14 |
| H30 | 150 | 155 | 1.03 |
| H29 | 150 | 173 | 1.15 |
| 静岡県私学協会の公開情報より | |||
専門対策の有効性
「入試問題の難度」の続きですが、出題様式と傾向が偏っていることと学校説明会で要点を教えてもらえるので、「対策」は容易な部類です。
全体的な難度が高いので「一般的・標準的な中学受験勉強」だと必要学習量は多くなりますが、専門対策だと学習負担を大きく減らすことができます。
静岡雙葉中学の入試問題分析(算数)
- 読解整理が必要な問題が低得点域からある。
- 試験時間に対して問題数が多い。(時間内完答は難)
- 出題傾向の偏りが大きい。
| 20% | 40% | 60% | 80% | 100% | |
|---|---|---|---|---|---|
| 配点 | D | D | C | C | B |
| 得点難度 | D | D | C | B | B |
| 合否ライン | 〇 | ||||
「文章」の読解が一苦労
日本語で書かれた文章を数式に置き換えていくのが数学ですが…そういう論点とは違う「読み難さ」があります。
過去問で慣れておかないとウンザリして問題解く気がなくなってしまいます。
国語の長文読解問題の負けパターンみたいですね!
図表による可視化が必要(論理系)
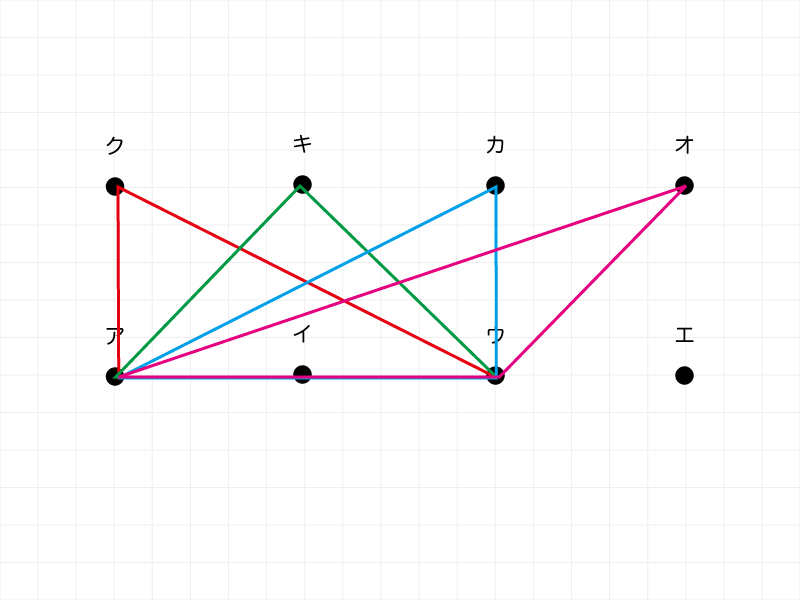
上記は、上下の点を結んでできる三角形の面積の和を求める問題です。(2016年出題)
組み合わせのパターンごとに面積の和を出して、合計することで求めます。(下表)
| 底辺 | 組 | 通数 | 1個面積 | 面積合計 |
|---|---|---|---|---|
| 1㎝ | 〔アイ〕〔イウ〕〔ウエ〕 | 3通り | 0.5c㎡ | 1.5c㎡ |
| 2㎝ | 〔アウ〕〔イエ〕 | 2通り | 1c㎡ | 2.0c㎡ |
| 3㎝ | 〔アエ〕 | 1通り | 1.5c㎡ | 1.5c㎡ |
| 合計 | 5c㎡ |
図表に書き出せば簡単そうですが、頭の中で処理するのは難しそう。
「点つなぎの組み合わせ」は定番ですが、そこに面積が加わると表などに書き出さないと計算漏れしやすいです。
論理の問題は時間をかければ解けるものも多いですが、だからといって10分20分かけてしまうと他の問題に手が回らなくなります。
ちなみに完答ペースでは、上記例題は6~7分で仕上げる必要があります。
出題傾向に偏りが大きい
傾向一覧は載せませんが、過去問の学習は裏切りません。
静岡雙葉中学を目指す場合の塾の選び方
- 個別指導塾が基本。
- 集団指導塾はお勧めできない。
集団指導塾が勧められない理由
塾の授業は図表を書き出しながら説明してくれるのですよね?
なのでそこは講師に任せて、板書と説明が終わってから手や頭を動かし始めるのです。
は?
それだと塾ではできても本番で点がとれないのでは?
もちろん集団指導塾に通う子の全員がそうであるわけではないですが、それが少数派であることは模試の成績表を見れば明らかです。
当塾にご依頼をご検討の方
| 取扱プラン | 標準プラン サテライトプラン(家庭教師) |
|---|---|
| 推奨開始学年 | 小学4年生1月~3月 |
| 6年生引受 | 条件付き可(6月末迄) |
静岡雙葉中学校・高等学校
県中部では唯一となる完全中高一貫女子校です。(高等部編入なし) 大学の推薦進学に有利な総合選択制のカリキュラム。
改変履歴
- 【2024.03.01】年度更新・文脈修正
- 【2023.01.29】新装版
- 【2022.09.28】改訂
- 【2022.03.24】改訂
- 【2021.05.26】初版
