2019年大問5:出会い算静岡雙葉中学過去問解説
2021.06.08
湖のまわりに、1周12㎞の道があります。ある地点からAさんとBさんが反対方向に、同時に出発して1周します。Aさんは時速6㎞の速さで50分歩いては、10分休みます。そしてまた50分、同じ速さで歩き10分休みます。これを繰り返します。Bさんは、時速4㎞の速さで1時間歩いては、5分休み、また同じ速さで1時間歩き、5分休みます。Bさんもこれを繰り返します。
【2019年】
高頻出問題です。
「出会い算」は2人がA地点とB地点それぞれから移動する速さの問題です。線分図で解く他に、グラフに書き出した状態を図形的にとらえて相似比を使うなどの様々な解き方があります。
多様性があるので数学好きな講師は生徒を置き去りにして異世界にいってしまうので、講師運がわるいと「わかったよーな、わからないよーな?」になりがちな問題です。
- 速さ(5年生)
- 難度目安 【 基礎 】
大問概要
・・・なんだか読むのも面倒ですね。というか、解き方を考えるときにこんなものをいちいち読み返していたらウンザリして当然です!
読むのがめんどくさくなって問題にきちんと取り組まない・・・という失点理由はとても多いです。
よってこの類の問題は、まず要点を抜き出すことが大事です。
湖のまわりに、1周12㎞の道があります。ある地点からAさんとBさんが反対方向に、同時に出発して1周します。Aさんは時速6㎞の速さで50分歩いては、10分休みます。そしてまた50分、同じ速さで歩き10分休みます。これを繰り返します。Bさんは、時速4㎞の速さで1時間歩いては、5分休み、また同じ速さで1時間歩き、5分休みます。Bさんもこれを繰り返します。
これを整理すると次のようになります。
- 1周12キロ
- Aは時速6キロで反時計回り。50分毎に10分停止。
- Bは時速4キロで反時計回り。60分毎に5分停止。
問題文を要約したら、ついでに数字の早見表をつくっておきましょう。
| A | B | |
|---|---|---|
| 時速 | 6㎞ | 4㎞ |
| 分速 | 100m | 200/3 m |
| 3分で | 300m | 200m |
| 10分で | 1㎞(1000m) | (計算略) |
| 15分で | 1.5㎞(1500m) | 1㎞(1000m) |
何を抜き出すかは小問をひととおり読めばわかると思いますが、あくまで下準備なので手を止めずできることに限定します。
小問1
Bが1周するのにかかる時間は、何時間何分ですか?
要点抜き出しなどの下準備をしていれば・・・
時速4キロで12キロ移動するのに何時間かかる?
・・・という、宿題の計算ドリルと同程度の問題であることがわかります。
つまりこの小問を解くために必要な学習は、知識ではなく「読解と下準備の習慣」です。
注意点
12キロを時速4キロなので3時間・・・ですが、1時間ごとに5分休憩をしています。
60分=1時間ごとに5分休憩で、3時間歩いたから、休憩した時間は〔5分×3回=15分〕
よって3時間+15分=3時間15分
・・・ではありません。
| 経過時間 | 0 | 1:00 | 1:05 | 2:05 | 2:10 | 3:10 | 3:15 |
|---|---|---|---|---|---|---|---|
| 歩いた距離 | 0 | 4キロ | 8キロ | 12キロ | 到着済 | ||
| ゴールまで | 12キロ | 8キロ | 4キロ | 0 | 休憩不要 | ||
3回目の休憩はゴールに到着した後になるのでノーカウントです。
道のり12㎞ ÷ 時速4㎞ + 休憩5分×2 = 3時間10分
小問2
Aさんが1周するのにかかる時間は、何時間何分ですか。
小問1と同じです。
道のり12㎞ ÷ 時速6㎞ + 休憩10分×2 = 2時間20分
ただし、この計算だと最後の休憩がゴールに到着する前なのか後なのかがわかりにくいので、表に書き出すほうが安心・安全です。
| 経過時間 | 0 | 0:50 | 1:00 | 1:50 | 2:00 | 2:10 | 2:20 | 2:30 |
|---|---|---|---|---|---|---|---|---|
| 分換算 | 0 | 50 | 60 | 110 | 120 | 130 | 140 | 150 |
| 歩いた距離 | 0 | 5キロ | 10キロ | 11キロ | 12キロ | |||
| ゴールまで | 12キロ | 8キロ | 4キロ | 1キロ | 到着 | |||
下準備で分速の早見表をつくっておくと表の穴埋めがスムーズにできると思います。
そしてこの表は、次の小問3で使います。
小問3
出発して1時間5分後には、Aさんは何㎞歩いていますか。
最初の下準備でつくった早見表と、小問2の表があるとデータを読み取るだけです。
小問2の表より、1時間経過したときは「5キロ地点」にいる
分速100mで5分移動するので=100×5=500m
つまり5キロ+0.5キロ=5.5㎞
計算で解く場合
分速100m 50分毎に休憩 その後10分休憩
つまり、60分(1時間)で移動する距離は、50分で移動する距離と同じ。
- 分速100m×50分=5000m
- 分速100m×5分=500m
5000m+500m=5500m
㎞で答える指示なので、5.5㎞
小問4
2人が出会うのは、出発してから何時間何分後ですか?
いわゆる「出会い算」ですが、この問題は「休憩」があるので計算のみで答えを出すのはちょっと難しいかもしれません。
やはり表に書き出すのがいいと思います
単純計算=A+B=6+4=10キロ 1時間で10キロ。1周12キロなので、1時間少々で出会うことがわかります。
1時間=60分少々で出会うので、60~90分付近を詳細に書ける表をつくってみます。考え方は出会い算なので、AとBの移動距離の合計が12キロになったところが当たりです。
休憩で停止している部分だけ注意しながら、まずは暗算で計算できる1㎞ごとに表を埋めてみます。
| 経過時間(分) | 50 | 60 | 65 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|
| Aの位置(㎞) | 5 | 5 | 6 | 7 | 8 | |
| Bの位置(㎞) | 4 | 4 | 5 | |||
| A+B | 9 | 12 |
細かく探す必要もなく答えが出てしまいました。
殆どの大問は図表式解答が認められていますので、この表を書いて「上の表のとおり~」でマルがもらえます。
| 経過時間(分) | 50 | 60 | 65 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|
| Aの位置(㎞) | 5 | 5 | 6 | 7 | 8 | |
| Bの位置(㎞) | 4 | 4 | 5 | |||
| A+B | 9 | 12 |
【答|1時間20分後】
計算で求める場合
とりあえず休憩しないものとして出会い算します。
Aは分速100m、Bは分速200/3m
Bが分数になっているのでAも通分して分速300/3mとしておきます。「3分速でA300、B200」としてもいいです。
A+B=500/3m
AとBは1分あたり〔500/3m〕ずつ近づいていきます。
道は12㎞=12000mなので・・・
12000m÷〔500/3〕=72
AとBは72分後に出会う・・・ただし休憩しなかった場合
これに休憩分を足せばいいのでしょうが、ちょっと不安です。(この問題はそのやり方だと正しい答えは出ないと思います)
そこで、出会い=距離が縮まっている状況をもういちど整理してみます。
- AとBが両方とも動いている
- Aは動いているが、Bは動いていない
- Aは動いていないが、Bは動いている
- AもBも動いていない
動いている状況はこの4通りあるので、それぞれについて距離の縮まりを計算します。
| 動き | ABの距離 | |
|---|---|---|
| 最初の50分 | AB両方動く | 〔500/3〕×50分=25000/3m |
| 50-60分 | Bだけ動く | 〔200/3〕×10分=2000/3m |
| 60-65分 | Aだけ動く | 〔300/3〕×5分=1500/3m |
| 65分~110分 | AB両方動く | 〔500/3〕×・・・ |
〔25000/3〕+〔2000/3〕+〔1500/3〕=〔28500/3〕=9500m
12000-9500=2500m
つまり、65分経過時点でABは合計9500m移動しており、残りは2500m
この2500mにかかる時間をAB両方動く分速〔500/3〕で計算します。
2500m÷〔500/3〕=15分
休憩は入らないので・・・
65分+15分=80分 → 1時間20分
状態のグラフ
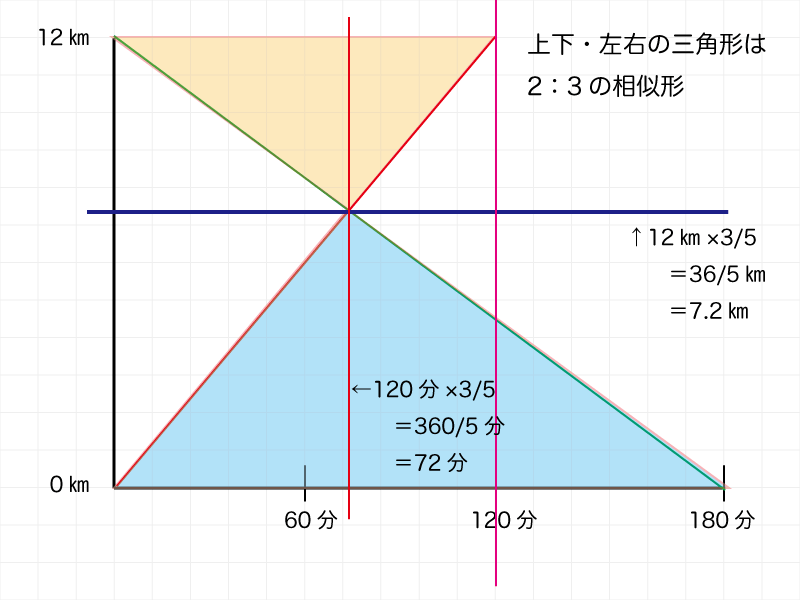
12000m÷〔500/3〕=72
AとBは72分後に出会う・・・ただし休憩しなかった場合
これをグラフに書き出すと次のようになります。
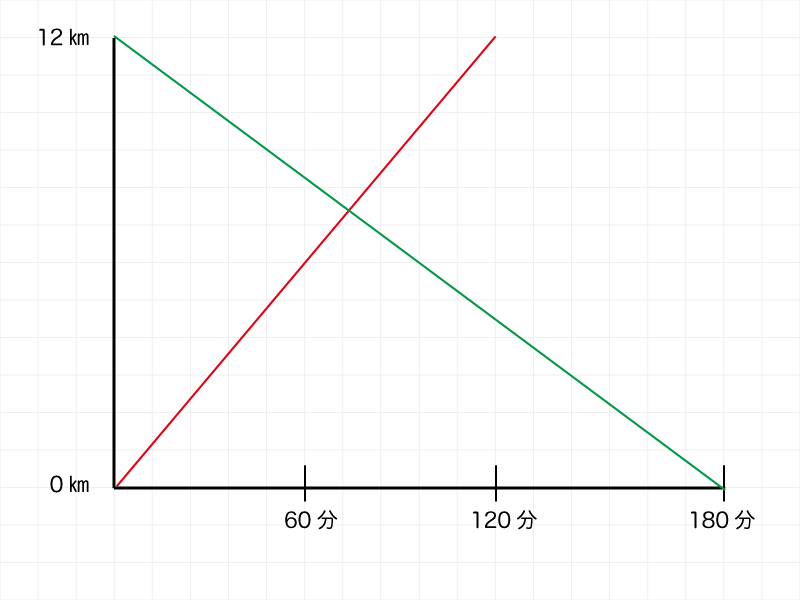
休憩していない問題なら、速さの比を使うことでグラフ上で出会った時間と位置がわかります。
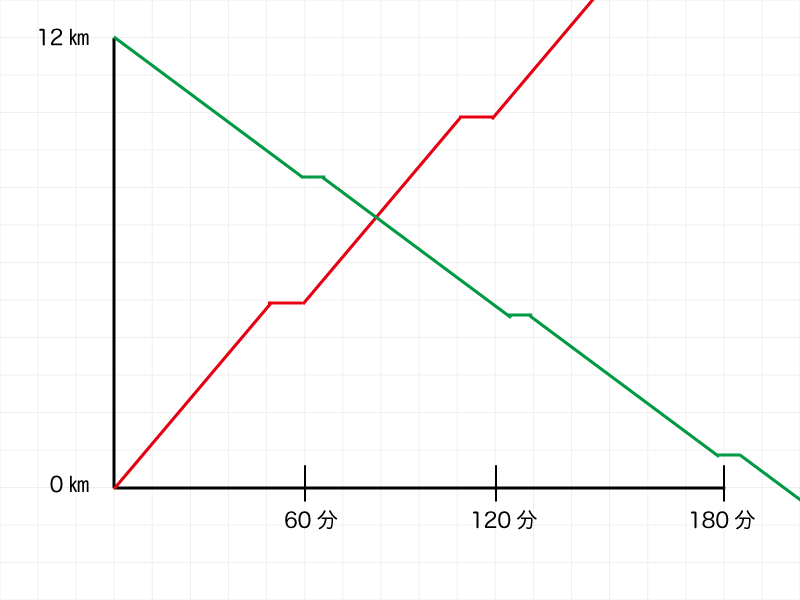
この問題のグラフは・・・
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)
