速さのグラフ静岡雙葉中学過去問解説
- 2021.10.13
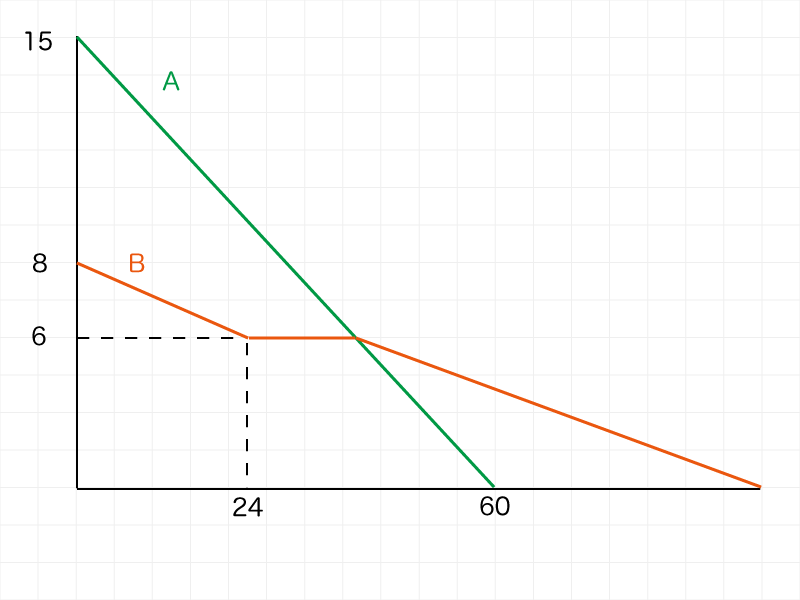
【問題文略】
2019年大問3
グラフから速さや時間を読み取る問題です。
ふつう
頻出(慣熟必須)
- 速さ(5年生)
小問1
ろうそくAとろうそくBは1分間にそれぞれ何㎝短くなりますか。分数で答えなさい。
グラフを読み取って速さを求めます。
ろうそくA(グラフA)
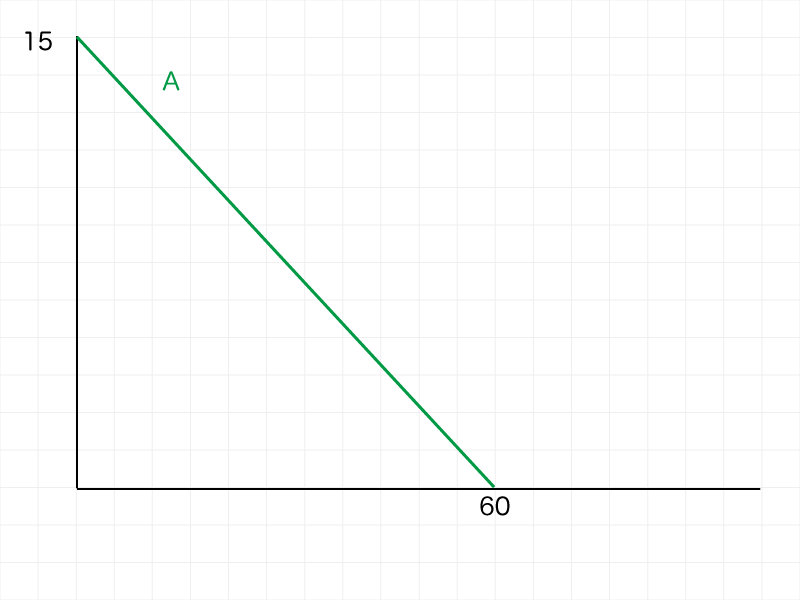
60分で15㎝進んでいます。
60分で15㎝ → 1分なら何㎝?
15㎝ × 1/60 = 15/60
約分して 1/4㎝/分
60÷15=4…などという適当な数字転がしはダメ
ろうそくB(グラフB)
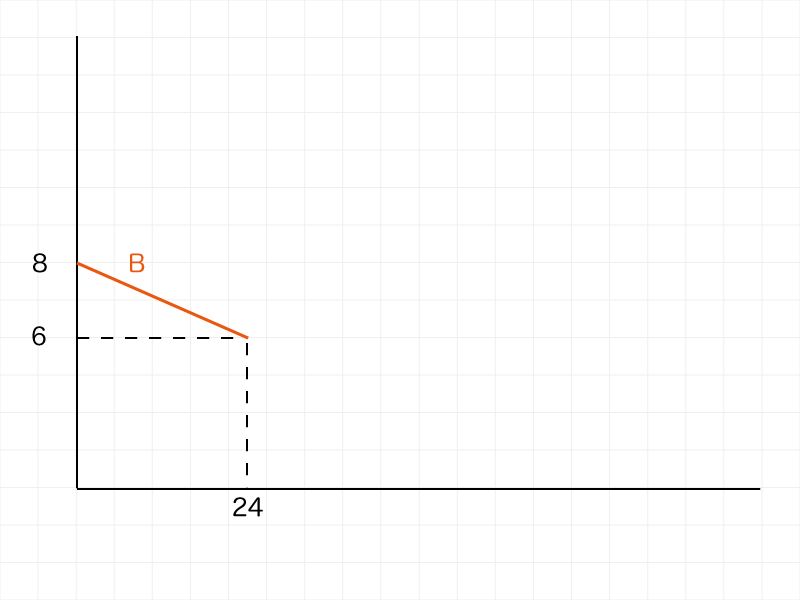
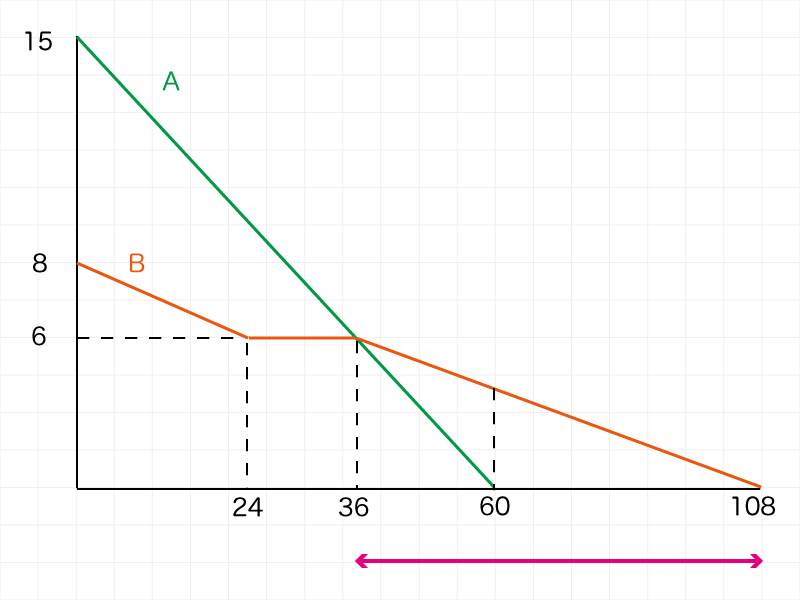
Bは上図の位置で読み取ります。
進んだ距離(減った長さ)は、8㎝ー6㎝=2㎝です。
2㎝進むのに24分かかっていますので・・・
24分で2㎝ → 1分なら何㎝?
2㎝ × 1/24 = 2/24
約分して 1/12㎝/分
まとめ
A:1/4㎝ B:1/12㎝
「わり算」より「分数のかけ算」がわかりやすいです。
小問2
ろうそくBの火は何分間、消えていましたか。
着目するのはAとBが同じ長さになっている箇所、グラフ上ではABが交差している箇所です。
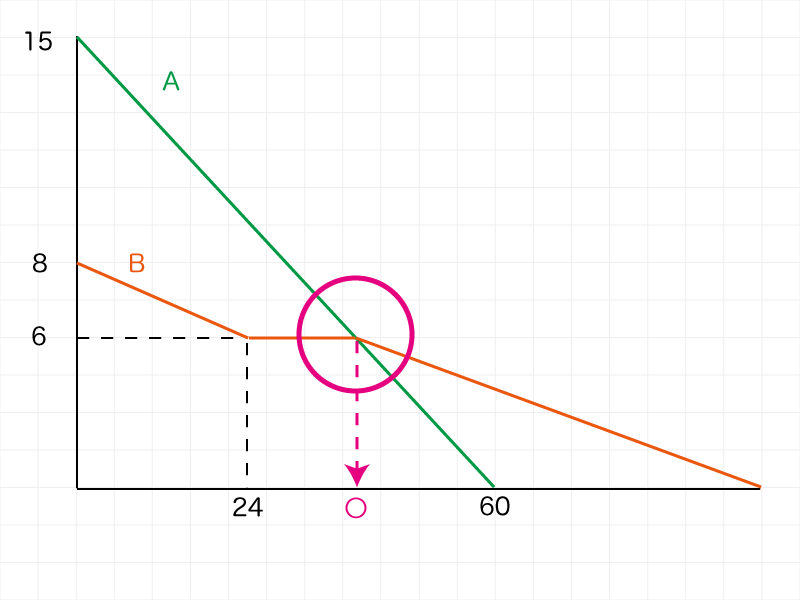
グラフにある情報からこの位置の「時刻(開始からの時間)」を求めて、ろうそくBの火が消えた時刻の「24」を引けば、消えていた時間が求められます。
Aの長さから時刻を求める
交差しているときの長さは6㎝であることが読み取れます。
このときまでにろうそくAが減った長さ、つまりAが進んだ距離は・・・
最初15㎝ ー 6㎝ = 9㎝
Aが9㎝進むためにかかる時間を求めれば、ABが交差している「時刻」がわかります。
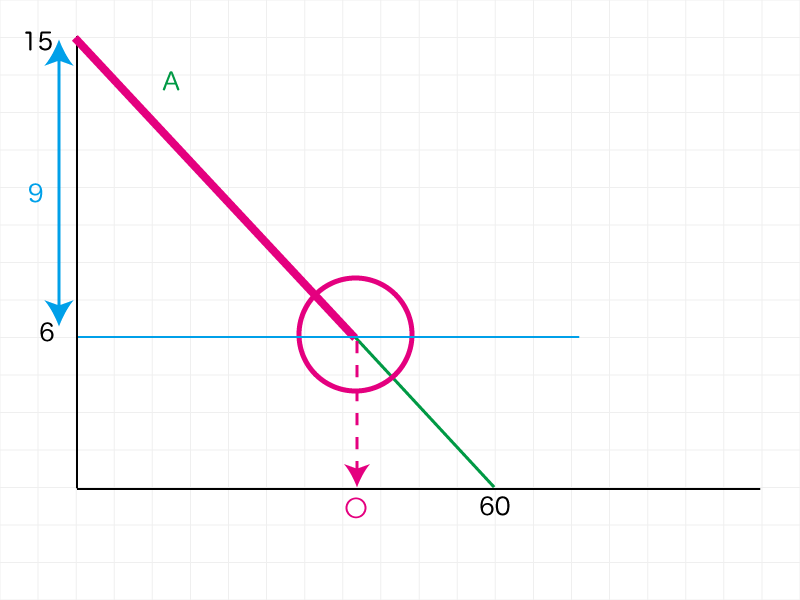
Aの速さは小問1で求めていますので・・・
9㎝ ÷〔1/4〕㎝ =36分
あるいは・・・
1/4㎝で1分 → 9㎝は何分?
1㎝で4分 → 9㎝は何分?
4分 × 9倍 = 36分
よってABが交差している箇所の「時刻」は36分であることがわかります。
これを必ずグラフに書き込みます!
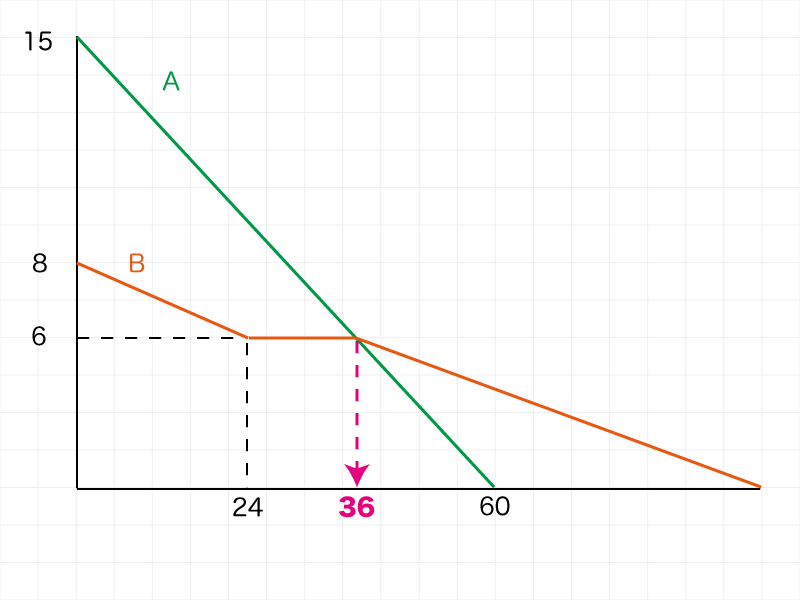
36分 ー 24分 = 12分
【別解】 グラフの形状から相似比で求める
グラフの状態を「図形」で考えます。
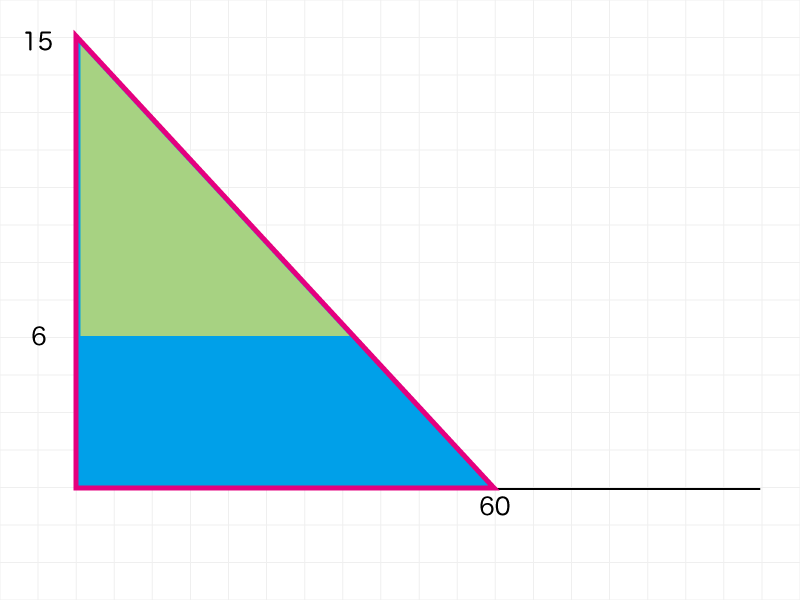
- A(青)の三角形:底辺60、高さ15
- B(緑)の三角形:底辺x、高さ9(15-6)
ABの三角形は相似なので、底辺の比と高さの比は同じです。
高さの比は〔15:9〕→〔5:3〕なので、底辺の比も〔5:3〕になります。
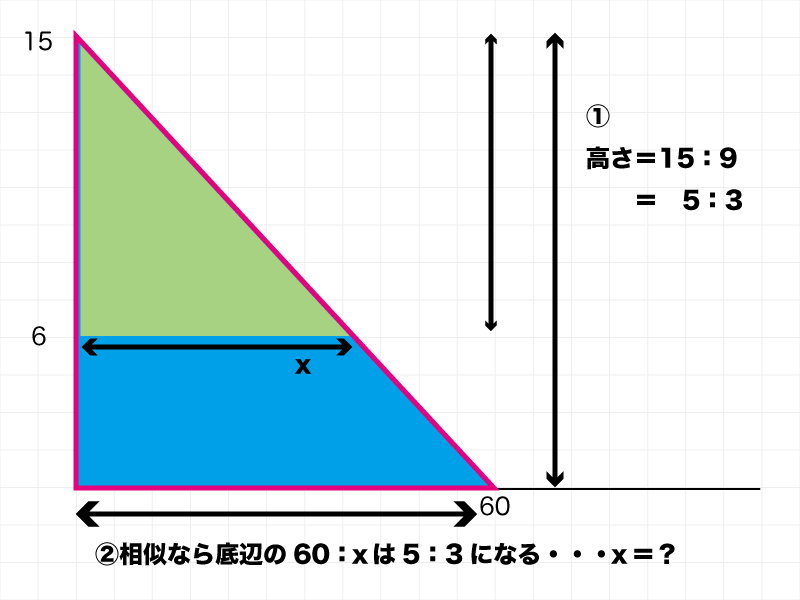
〔5:3〕=〔60:x〕
x=36
ABが交差している箇所までの長さは「36」です。
相似のしくみを使うと解答スピードが大幅に上がるので、高得点狙いでは必携知識といえます。
ですが、それはあくまでグラフから「速さ・距離・時間」の関係を瞬時に読み取れる場合に限った話です。
小問3
ろうそくBの火は、ろうそくAの火が消えてから何分後に消えましたか。
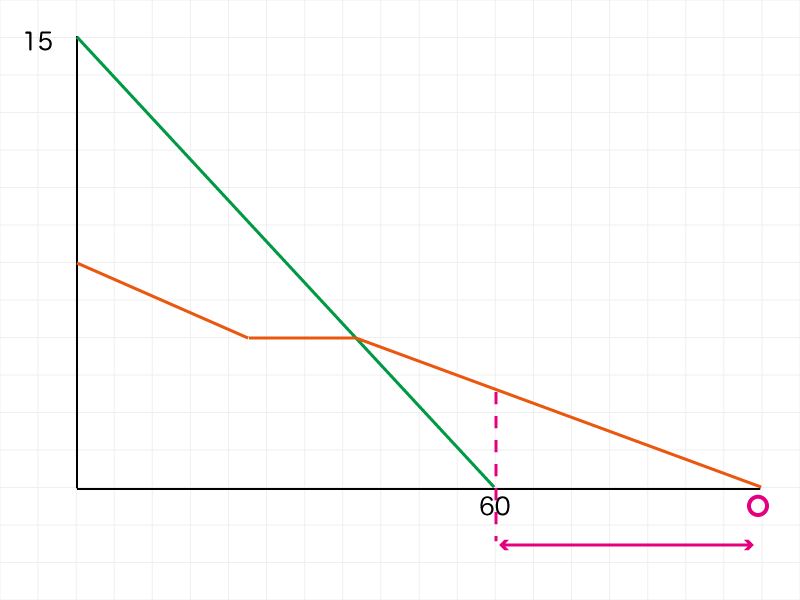
解き方の流れは基本どおりですが、計算の開始点が二転三転します。
どこを計算しているのかをハッキリわかるように計算過程を残すことが重要です。
Aが消えたときのBの残り長さを求める
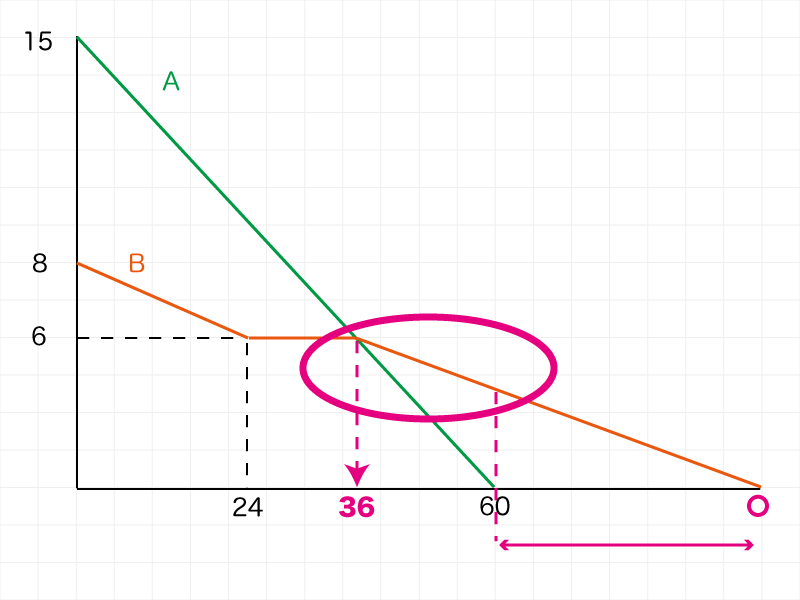
小問2によって開始時刻がわかり、Aが消えた時刻は問題文で与えられています。
ここまでの結果をグラフに書き込んでいれば一目瞭然です。
小問1によって速さもわかっていますので、この時間で何センチ進む(残りが減る)かは計算できます。
| 開始 | 終了 | 変化 | |
|---|---|---|---|
| 長さ(距離) | 6㎝ | 欲しい情報 | 計算で求める |
| 時刻 | 36分 | 60分 | 24分 |
分速〔1/12〕㎝ で24分進んだので、
〔1/12〕㎝ × 24分 = 2㎝
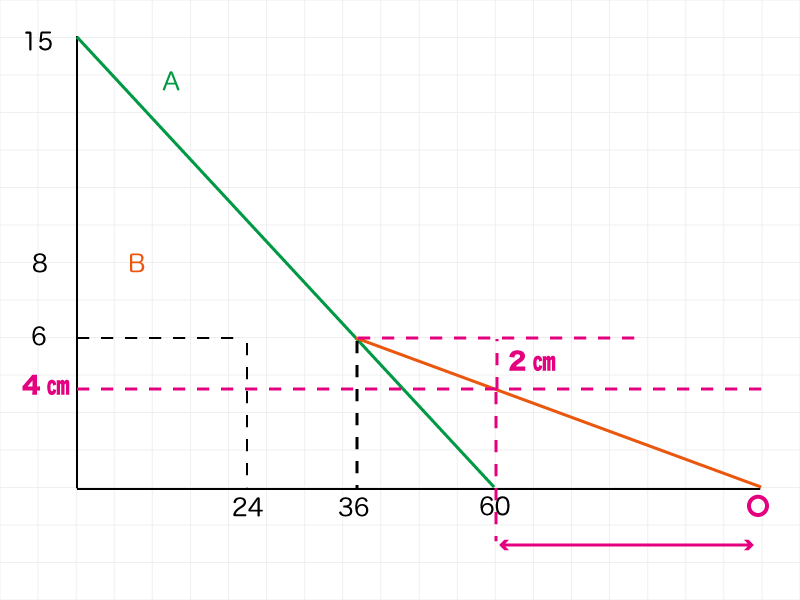
Aが消えたときにBは4センチになっていることがわかります。
残り4センチについて、分速1/12センチで何分かかるか?
4㎝ ÷〔1/12〕=48分
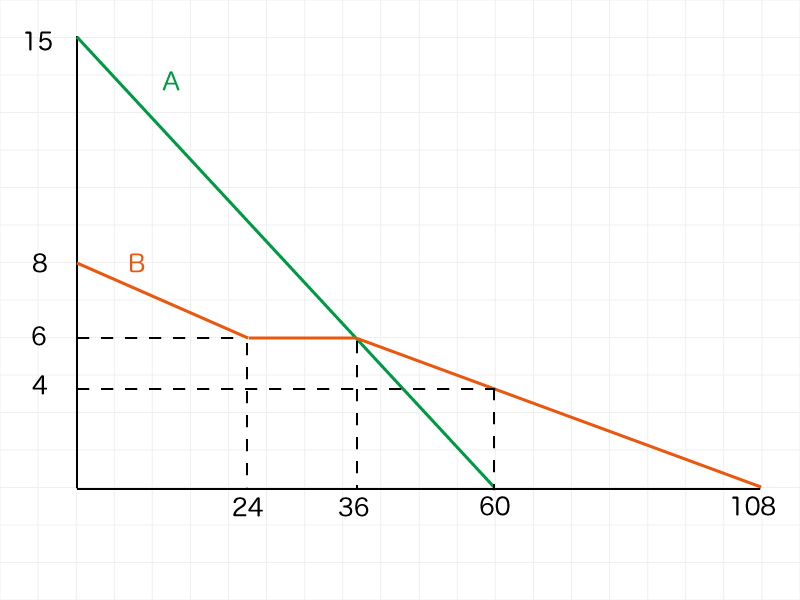
【別解】小問2の時刻からBが消えるまでの時間を計算する
まず、小問2で求めた時刻の長さ(6㎝)から最後(0㎝)までにかかる時間を求めます。
6㎝ ÷〔1/12〕㎝ = 72分
開始の「時刻」は36分なので、この72分を足せばBが消えた「時刻」がわかります。
36+72=108
ただし、これは「6㎝のろうそくが消えるまでの『経過時間』」です。
問われているのは「Aが消えてから何分後?」です。Aが消えた「時刻」は60分、Bが消えた「時刻」は108分なので・・・
108分 ー 60分 = 48分後
余談
「速さとグラフ」の問題を解くポイントは・・・
- 自分が何を求めているか明確にしながら計算する。
- 移動の「時間」と、開始から経過した「時刻」を混同しない。
- 時刻(横X軸)と距離(縦Y軸)を求めたら、必ずグラフに書き込む
「速さのグラフ」はほぼ毎年出題されています。
努力がスコアになりやすい「お得な単元」です。
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)
