2016年大問5:組み合わせと面積の複合問題静岡雙葉中学過去問解説
縦、横、それぞれ1㎝おきに点アから点クまでの8個の転が下の図のように並んでいます。また、点アから順番に転を結んでできる四角形アエオクは長方形になります。この中から3つの点を選んで三角形をつくります。たとえば点アと点ウと点キを選ぶと、三角形アウキができます。
組み合わせの問題に三角形の等積変形が混じる少し難度が高い問題です。
- 組み合わせ(6年)
- 三角形の面積(5年)
- 等積変形
- 難度目安 【 標準 】
状況整理
解き始める前に状況を整理しながら視覚的に確認します。
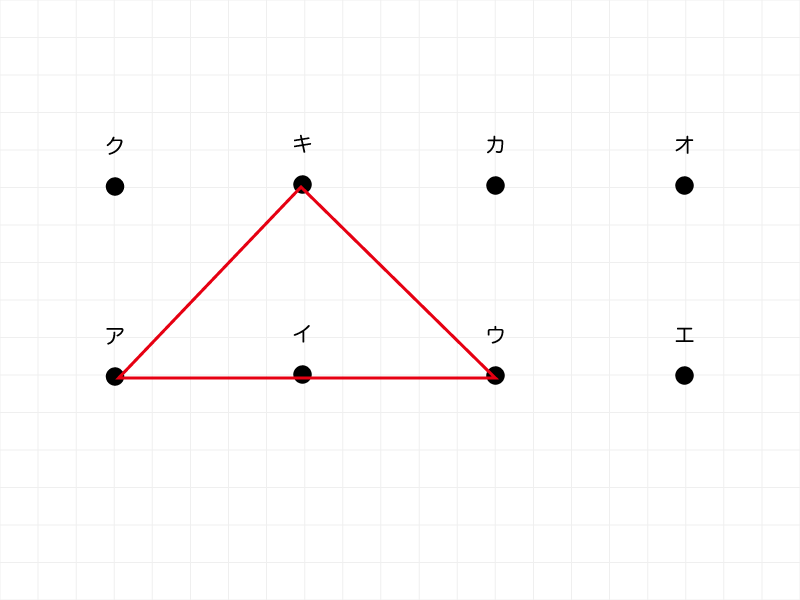
この問題は、下段「アイウエ」か上段「クキカオ」のいずれか2点と、反対側の上段か下段の1点の組み合わせを考えます。
小問1
アイを1辺とする三角形を全て書きなさい。
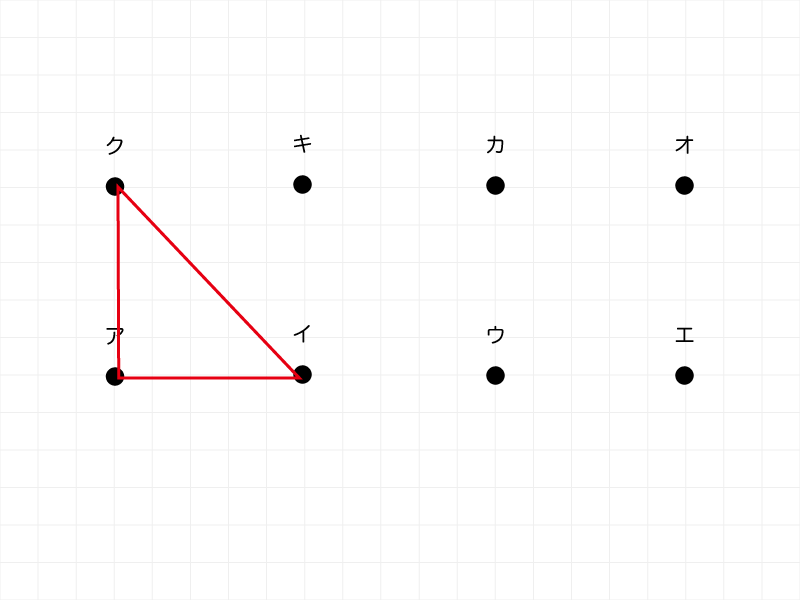
「アイを1辺とする三角形」の1つは上図のようになります。
下段は三角形の底辺として〔アイ〕が固定なので、頂点となる上段の組み合わせが何通りあるかという問題です。
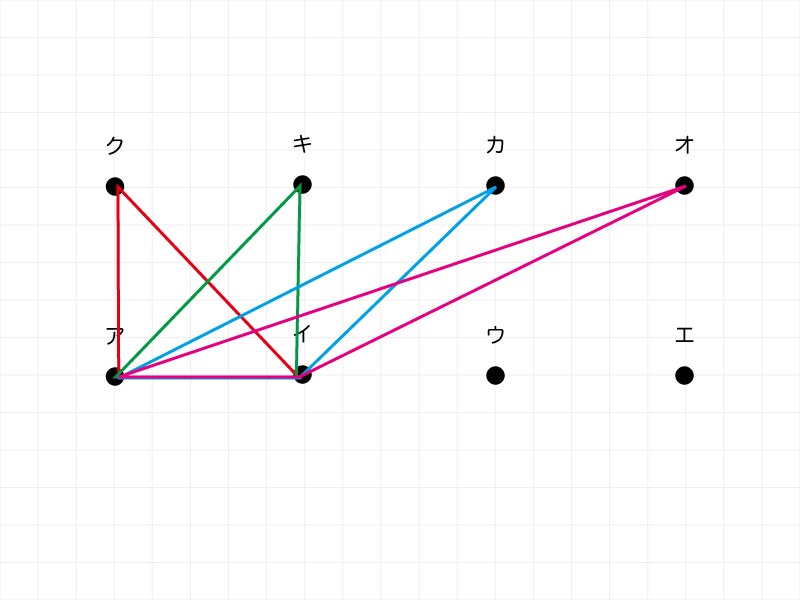
〔アイク〕〔アイキ〕〔アイカ〕〔アイオ〕
小問2
面積が1c㎡となる三角形は全部で何個できますか?
まず、「面積が1c㎡となる三角形」の形状を確認します。
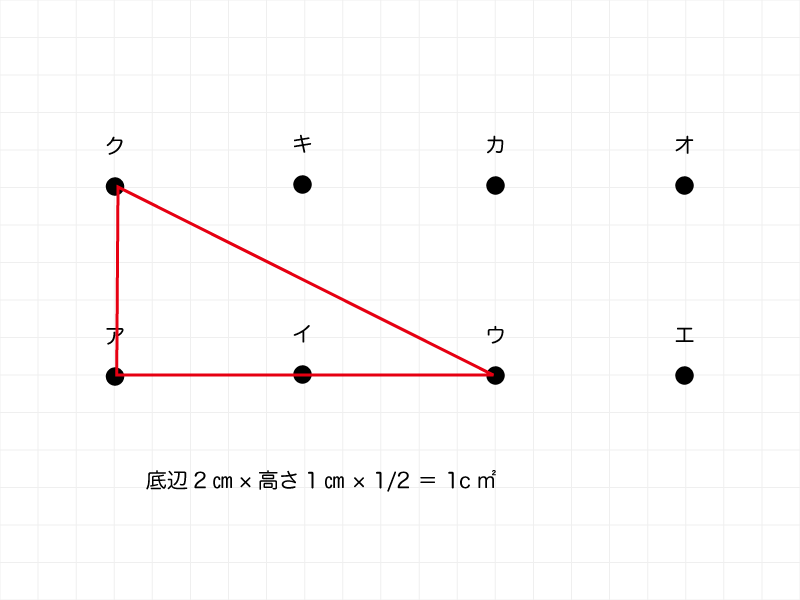
高さは1㎝で固定なので、底辺は・・・上図のようになります。
- 底辺になるものは、下段〔アウ〕と〔イエ〕の2通り
- このときもうひとつの頂点になるものは、それぞれ〔オ〕〔カ〕〔キ〕〔ク〕の4通りある。
- この4通りの面積は全て同じ。(底辺と高さが同じ)
- 上段を底辺とした組み合わせも同様。
〔下段底辺2通り〕×〔頂点4通り〕×〔上下逆2〕=16個。
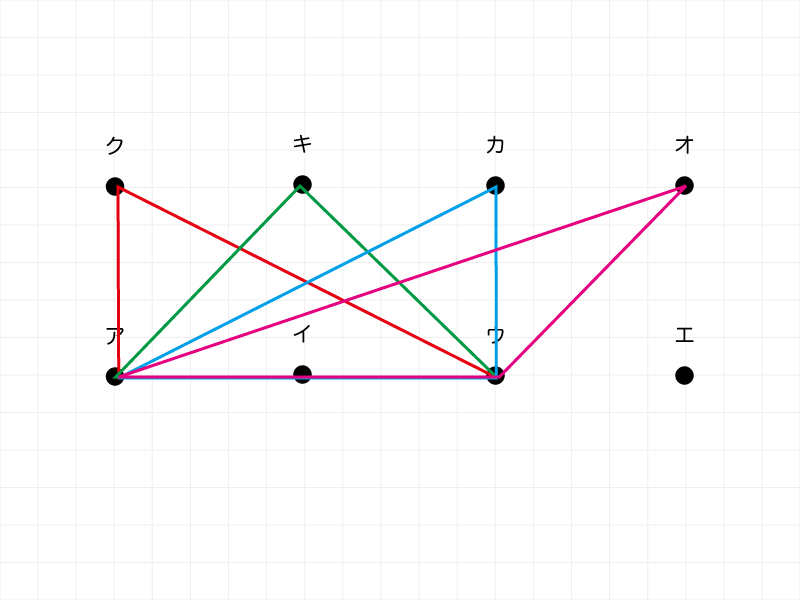
上段が底辺となる組み合わせ例
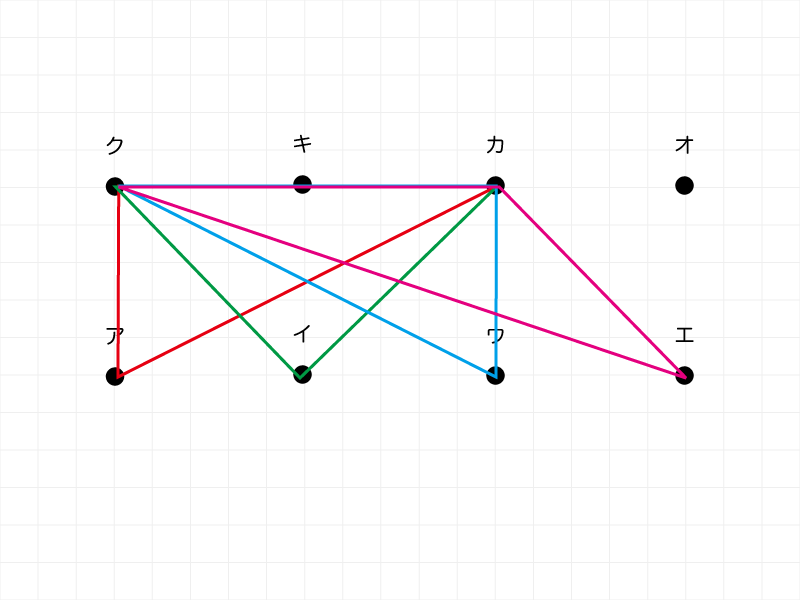
小問3
3つの点を結んでできる、すべての三角形の面積の合計を求めたいと思います。
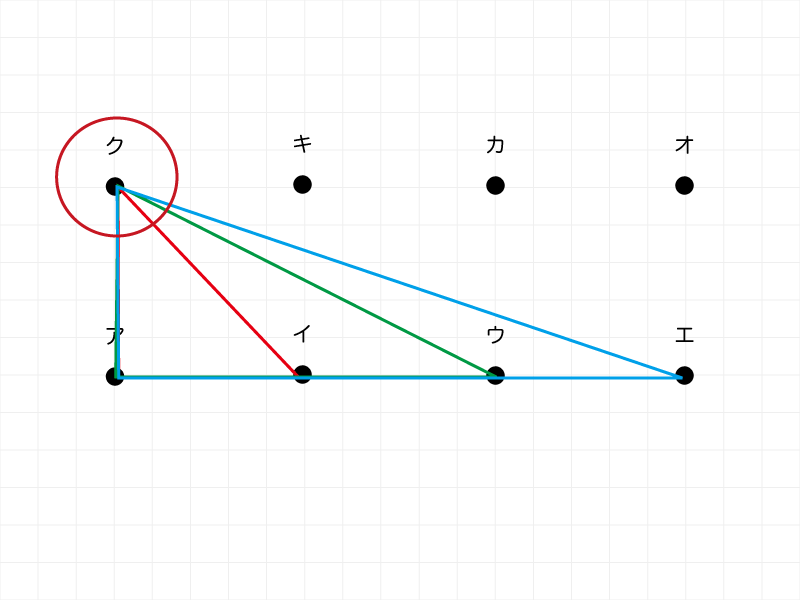
小問2までは「底辺」を元にして考えましたが、ここからは「底辺ではない頂点」を元にします。
〔3-1〕三角形は全部で何個できますか。
「上段ク」を頂点としたとき、底辺になるものは、長さがそれぞれ「1㎝」「2㎝」「3㎝」の組み合わせがあります。
まずはそれを表に書き出します。
| 長さ | 組 | 通数 |
|---|---|---|
| 長さ1㎝ | 〔アイ〕〔イウ〕〔ウエ〕 | 3通り |
| 長さ2㎝ | 〔アウ〕〔イエ〕 | 2通り |
| 長さ3㎝ | 〔アエ〕 | 1通り |
「上段ク」を頂点にしたときにつくれる三角形はぜんぶで6通りあります。
他の頂点でも同様であり、頂点が下段にうつると底辺は上段にうつります。要するに、各頂点に対して6通りの三角形がつくれます。
6通り×8頂点=48個
〔3-2〕全ての三角形の面積の合計を求めなさい。
先ほどつくった表に追記します。
| 長さ | 組 | 通数 | 1個面積 | 面積合計 |
|---|---|---|---|---|
| 長さ1㎝ | 〔アイ〕〔イウ〕〔ウエ〕 | 3通り | 0.5c㎡ | 1.5c㎡ |
| 長さ2㎝ | 〔アウ〕〔イエ〕 | 2通り | 1c㎡ | 2.0c㎡ |
| 長さ3㎝ | 〔アエ〕 | 1通り | 1.5c㎡ | 1.5c㎡ |
| 合計 | 5c㎡ |
これが頂点8個分あるので・・・
5c㎡×8通り=40c㎡
余談
図入りで通して解説すると簡単に見えますが、実際のテストで出題されるとかなり難しいのではないかと思います。
この解説は「底辺×高さが同じ=等積変形」の考え方で組み合わせを整理していますが、問題を見てすぐにそれに気づけば解説の印象どおりさほど難しくないですが、小問2を解いている最中に気づけないと終わりの見えない試行錯誤にハマってしまうと思います。
静岡雙葉中学の受験を検討中の方

入試傾向と対策学習のご案内はこちら。
サブコンテンツ全体の刷新作業を行っています。
2022年11月23日から2023年3月末頃(予定)
